
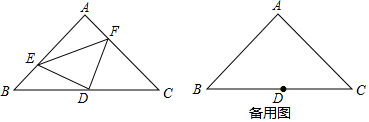
分析 (1)利用等腰直角三角形的性质得出AD=BD=DC,进而证明△AED≌△CFD,利用全等三角形的性质得出DE=DF,∠ADE=∠CDF进而得出△DEF为等腰直角三角形;
(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,首先利用已知得出AD=BD=DC,进而利用全等三角形的判定得出△AED≌△CFD.
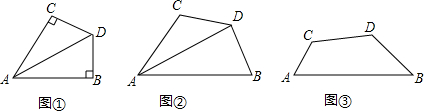
解答 解:(1)如图①,结论:DE=DF.DE⊥DF,
理由:连接AD,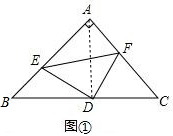
∵∠BAC=90°,AB=AC,D为BC中点,
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAD=∠DAC}\\{AD=DC}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF+∠ADF=90°,
∴∠ADE+∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF.
(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,如图②,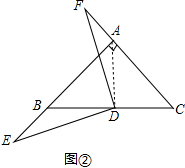
理由:∵∠BAC=90° AB=AC,D为BC中点
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAD=∠C}\\{AD=CD}\end{array}\right.$,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF-∠ADF=90°,
∴∠ADE-∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题,体会这类题目形变结论不变,证明方法完全类似,属于中考常考题型.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
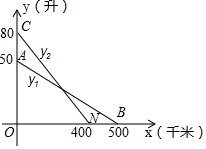 如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
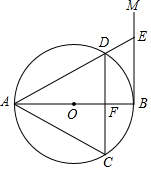 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
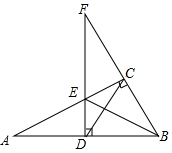 在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于点F,连接CD、BE,若EF=AE.
在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于点F,连接CD、BE,若EF=AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
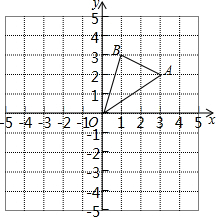 如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.
如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com