
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=![]() ,tan∠DBC=
,tan∠DBC=![]() .
.
求:(1)边CD的长;
(2)△BCE的面积.
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AC∥x轴,点B在第四象限,AO平分∠BAC,AB交x轴于G,连OB,OC.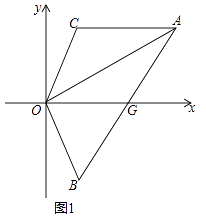
(1)判断△AOG的形状,并证明;
(2)如图1,若BO=CO且OG平分∠BOC,求证:OA⊥OB;
(3)如图2,在(2)的条件下,点M为AO上的一点,且∠ACM=45°,若点B(1,﹣2),求M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.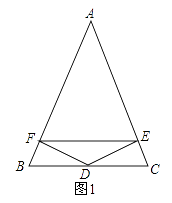
(1)求证:AE=AF;
(2)如图2,若∠BAC=60°,△ABD的面积为4,连接AD交EF于M,连接BM、CM,在不添加任何辅助线的情况下,请直接写出图中所有面积为1的三角形.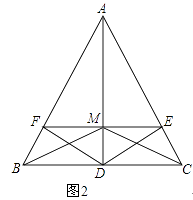
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(1)如图①,当点H与点C重合时,可得FGFD.(大小关系)
(2)如图②,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.
(3)在图②中,当AB=8,BE=3时,利用探究的结论,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将放置于直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A1OB1.已知∠AOB=30°,∠B=90°,AB=1,则B1点的坐标为( )

A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D (
) D (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com