
| A. | y是x的一次函数 | B. | y与x没有函数关系 | ||
| C. | y是x的函数,但不是一次函数 | D. | y是x的正比例函数 |
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
 如图:在矩形ABCD中,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向C点移动,同时动点Q以1m/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动的时间为t秒(0<t<5).
如图:在矩形ABCD中,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向C点移动,同时动点Q以1m/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动的时间为t秒(0<t<5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
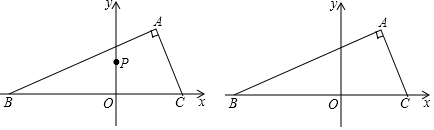
 如图,在△ABC中,∠C=90°,∠B=30°,O为AB上一点,AO=k,⊙O的半径为1.问k为何值时,⊙O与AC:
如图,在△ABC中,∠C=90°,∠B=30°,O为AB上一点,AO=k,⊙O的半径为1.问k为何值时,⊙O与AC:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
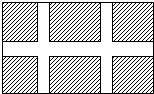 如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com