
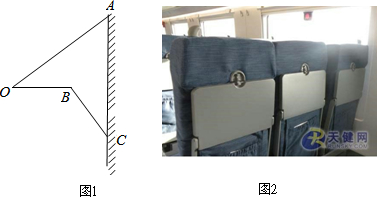
分析 (1)如图延长CB交OA于E,根据∠OBC=∠AOB+∠BEO即可计算.
(2)延长OB交AC于F.设BC=x,则OB=OA-BC=75-x,在RT△BCF中求出BF,再在RT△AOF中根据cos37°=$\frac{OF}{AO}$,列出方程即可解决问题.
解答 解:(1)如图延长CB交OA于E,
∵OA⊥BC,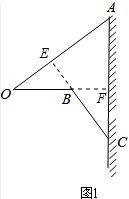
∴∠BEO=90°,
∵∠AOB=37°,
∴∠OBC=∠AOB+∠BEO=37°+90°=127°.
(2)延长OB交AC于F.设BC=x,则OB=OA-BC=75-x,
∵∠AOB=∠ACB,∠OBE=∠CBF,∠AOB+∠OBE=90°,
∴∠ACB+∠CBF=90°,
∴∠BFC=90°
在Rt△BFC中,∵sin37°=$\frac{BF}{BC}$,
∴BF=0.6x,OF=75-0.4x,
在RT△OAF中,cos37°=$\frac{OF}{OA}$,
∴$\frac{75-0.4x}{75}$=0.8,
∴x=37.5厘米.
∴小桌板桌面的宽度BC的长度为37.5厘米.
点评 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是添加辅助线构造直角三角形解决问题,学会设未知数,用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 为便民惠民,人民公园特推出下列优惠方案:
为便民惠民,人民公园特推出下列优惠方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
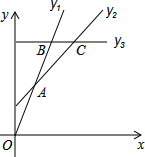
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
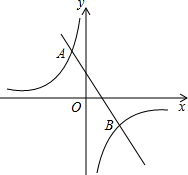
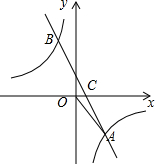 如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.
如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com