
| A�� | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ |
���� ���÷Ǹ����������г������飬���������Ľ⼴�ɵõ�a��b��ֵ��
��� �⣺��|3a-2b-12|+��a+2b+4��2=0��
��$\left\{\begin{array}{l}{3a-2b=12}\\{a+2b=-4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$��
��ѡ��B��
���� ���⿼���˽��Ԫһ�η����飬��������Ԫ��˼�룬��Ԫ�ķ����У�������Ԫ����Ӽ���Ԫ����


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �����豸 | ���� | ���� |
| �۸���Ԫ/̨�� | 12 | b |
| ��������/�� �� | 240 | 180 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
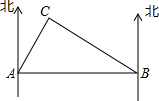 ��ͼ�������庣���ϣ�һ�ҽ�ž������ڻ���A�����������Ҿ�A��60�����B��ѵ����ͻȻ�ӵ��������Ҫ�ý�ǰ��C��������һ����Σ��������ҽԺ���Σ���֪C����A�ı�ƫ��30�㷽������B�ı�ƫ��60�㷽������B��������ƽ��ÿСʱ��ʻ30�����Ҫ����ʱ����ܰѻ��������͵�����ҽԺ������ȷ��0.1Сʱ��$\sqrt{3}$��1.7��
��ͼ�������庣���ϣ�һ�ҽ�ž������ڻ���A�����������Ҿ�A��60�����B��ѵ����ͻȻ�ӵ��������Ҫ�ý�ǰ��C��������һ����Σ��������ҽԺ���Σ���֪C����A�ı�ƫ��30�㷽������B�ı�ƫ��60�㷽������B��������ƽ��ÿСʱ��ʻ30�����Ҫ����ʱ����ܰѻ��������͵�����ҽԺ������ȷ��0.1Сʱ��$\sqrt{3}$��1.7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
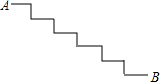 ��ͼ����̨��ʾ��ͼ����֪ÿ��̨�Ŀ��ȶ���30cm��ÿ��̨�ĸ߶ȶ���15cm������AB����AB���ڣ�������
��ͼ����̨��ʾ��ͼ����֪ÿ��̨�Ŀ��ȶ���30cm��ÿ��̨�ĸ߶ȶ���15cm������AB����AB���ڣ�������| A�� | 195cm | B�� | 200cm | C�� | 205cm | D�� | 210cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{2}$-$\sqrt{2}$=3 | B�� | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | C�� | 5$\sqrt{2}$��$\sqrt{2}$=6$\sqrt{2}$ | D�� | $\sqrt{8}$$��\sqrt{2}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 5�� | C�� | 3�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com