
 如图所示,设P为等边△ABC内的一点,且PB=2
如图所示,设P为等边△ABC内的一点,且PB=2| 2 |
| 2 |
| 2 |
| 2 |
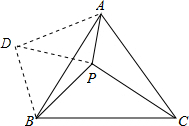 把△BPC绕B点逆时针旋转60°可得到△BDA,如图,
把△BPC绕B点逆时针旋转60°可得到△BDA,如图,| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源:数学教研室 题型:044
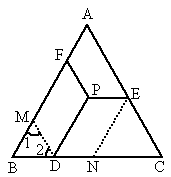
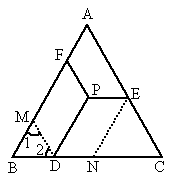
在一块等边三角形的草坪上,修建了一座凉亭,地点设为P,并从P点出发,分别修出一条通往等边三角形边缘的小路,为了美观,修小路要求PE∥BC、PD∥AB、PF∥AC,如图所示,若已知等边三角形的周长为1800m.
求:(1)三条小路PE、PD、PF的和;
(2)如果小路宽均为1m,每块砖的正面面积为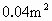 ,求需要多少块砖?
,求需要多少块砖?
查看答案和解析>>
科目:初中数学 来源: 题型:044
在一块等边三角形的草坪上,修建了一座凉亭,地点设为P,并从P点出发,分别修出一条通往等边三角形边缘的小路,为了美观,修小路要求PE∥BC、PD∥AB、PF∥AC,如图所示,若已知等边三角形的周长为1800m.
求:(1)三条小路PE、PD、PF的和;
(2)如果小路宽均为1m,每块砖的正面面积为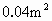 ,求需要多少块砖?
,求需要多少块砖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com