
【题目】已知方程组 ![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
【答案】
(1)解:解这个方程组的解为 ![]() ,
,
由题意,得 ![]() ,
,
不等式①的解集是:a≤3,
不等式②的解集是:a>﹣2,
则原不等式组的解集为﹣2<a≤3
(2)解:∵不等式(2a+1)x>(2a+1)的解为x<1,
∴2a+1<0且﹣2<a≤3,
∴在﹣2<a<﹣ ![]() 范围内的整数a=﹣1
范围内的整数a=﹣1
【解析】(1)先把a当作已知求出x、y的值,再根据x、y的取值范围得到关于a的一元一次不等式组,求出a的取值范围即可;(2)根据不等式2ax+x>2a+1的解为x<1,得出2a+1<0且﹣2<a≤3,解此不等式得到关于a取值范围,找出符合条件的a的值.
【考点精析】本题主要考查了一元一次不等式的整数解和一元一次不等式组的解法的相关知识点,需要掌握大大取较大,小小取较小;小大,大小取中间;大小,小大无处找;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有客房50间,当每间客房每天的定价为220元时,客房会全部住满;当每间客房每天的定价增加10元时,就会有一间客房空闲,设每间客房每天的定价增加x元时,客房入住数为y间.
(1)求y与x的函数关系式(不要求写出x的取值范围);
(2)如果每间客房入住后每天的各种支出为40元,不考虑其他因素,则该宾馆每间客房每天的定价为多少时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)+( ![]() m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数yl=x(x≥0), ![]() (x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
(x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
②当x>3时,y2>y1;
③当x=1时,BC=8;
④当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
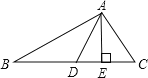
【题目】已知如图所示 AD、AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,,则△ABD与△ACD的周长之差为_________,△ABD与△ACD的面积关系为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com