
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
与x轴交于点A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
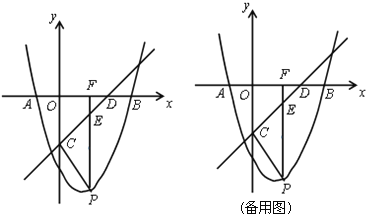
(1)求抛物线的解析式:
(2)若PE=3EF,求m的值;
(3)连接PC,是否存在点P,使△PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.
【答案】(1)y=x2-2x-3;(2)m=1或m=![]() ;(3)m=1±
;(3)m=1±![]() ,或
,或![]() 或
或![]() .
.
【解析】
试题分析:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,等腰直角三角形的性质,难点在于(3)判断出直线CD与y轴的夹角为45°并分情况讨论.
(1)将点A、B的坐标代入抛物线求出a、b,即可得解;
(2)根据抛物线解析式与直线解析式表示出点P、E的坐标,然后表示出PE、EF,再列出绝对值方程,然后求解即可;
(3)根据直线解析式求出直线CD与y轴的夹角为45°,然后分①∠PCE=90°时表示出PC的解析式,再与抛物线解析式联立求解即可;②∠CPE=90°时,PC∥x轴,点P与点C的纵坐标相等,然后根据抛物线解析式求解即可.
试题解析:(1)把A(-1,0)、B(3,0),两点的坐标代入y=ax2+bx-3得:![]() ,
,
解得:![]() ,
,
所以,这条抛物线的解析这式为:y=x2-2x-3;
(2)设点P的横坐标是m,则P(m,m2-2m-3),E(m,m-2),F(m,0),
PE=|yE-yP|=|(m-2)-(m2-2m-3)|=|-m2+3m+1|,
EF=|-m+2|,
由题意PE=3EF,即:|-m2+3m+1|=3|-m+2|,
①若-m2+3m+1=3(-m+2),整理得:m
②若-m2+3m+1=-3(-m+2),整理得:m2-7=0,
解得:m=7或m=-7,
∵P在x轴下方,
∴-1<m<3,m=-7不合题意应舍去,
∴m=7,
综上所述,m=1或m=7;
(3)存在点P的横坐标为:m=1-![]() 或
或![]() 或
或![]() .
.
理由如下:直线y=x-2与y轴的夹角为45°,
①PCE=90°时,直线PC的解析式为y=-x-2,
联立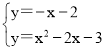 ,
,
消掉y得,x2-x-1=0,
解得x=![]() 或
或![]() ,
,
所以,点P的横坐标m=![]() 或
或![]() ;
;
②∠CPE=90°时,PC∥x轴,
∵点C(0,-2),
∴点P与点C的纵坐标相等,为-2,
∴x2-2x-3=-2,
解得x=1±![]() ,
,
∵点P是x轴下方的抛物线上一动点,
∴-1<x<3,
∴点P的横坐标m=1±![]() ,
,
综上所述,点P的横坐标m=1±![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
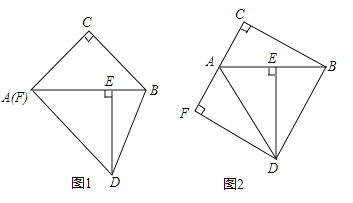
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
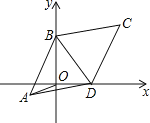
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题11分)完成下列推理说明:
(1)如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下:
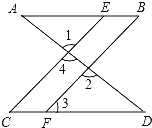
因为∠1=∠2(已知),且∠1=∠4(___________)
所以∠2=∠4(等量代换)
所以CE∥BF(___________)
所以∠___=∠3(_________________)
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD(______________________))
(2)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
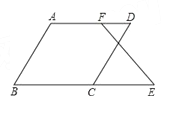
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD (__________)
∴∠B= ____(_______________________)
又∵∠B=∠D( 已知 ),
∴ ∠_____= ∠__________ ( 等量代换 )
∴AD∥BE(_____________________)
∴∠E=∠DFE(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年4月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.
(1)今年4月份A款汽车每辆售价为多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为6.5万元,B款汽车每辆进价为5万元,公司预计用不少于90万元且不多于96万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为7万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所购进汽车全部售完,且所有方案获利相同,a的值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com