

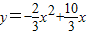 (2分);
(2分);
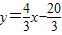
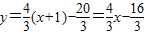 (1分)
(1分)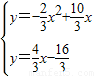 的解(1分)
的解(1分)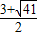 ,
,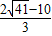 )(1分).
)(1分).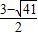 ,
, )不合题意舍去)
)不合题意舍去)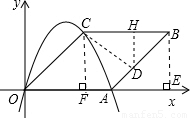 作CD⊥AB于D,作DH⊥BC于H,
作CD⊥AB于D,作DH⊥BC于H,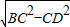 =3,
=3,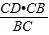 =
= ,
, ,则点D的纵坐标为
,则点D的纵坐标为
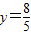 时
时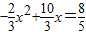

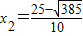
 上有一点(
上有一点( ,
, )
)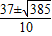 每对一个得(2分).
每对一个得(2分).

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
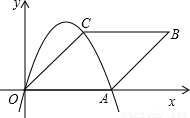
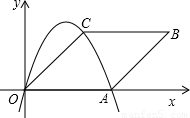
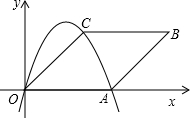 .抛物线y=ax2+bx+c过点O、A、C.
.抛物线y=ax2+bx+c过点O、A、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
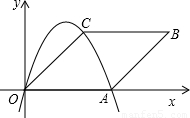
 .抛物线y=ax2+bx+c过点O、A、C.
.抛物线y=ax2+bx+c过点O、A、C.查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷30( 进化镇中 王士锋、向仕军)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(金山学校 来小权)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com