练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有大小两种货车，1辆大货车与3辆小货车额定载重量的总和为23吨，2辆大货车与5辆小货车额定载重量的总和为41吨. 1辆大货车、1辆小货车的额定载重量分别为多少吨？设1辆大货车的额定载重量为x吨，1辆小货车的额定载重量为y吨，依题意，可以列方程组为__________.

    【答案】

    【解析】

    设1辆大货车的额定载重量为x吨，1辆小货车的额定载重量为y吨，

    根据题意1辆大货车与3辆小货车额定载重量的总和为23吨，可列；根据题意2辆大货车与5辆小货车额定载重量的总和为41吨，可列，则可得答案.

    设1辆大货车的额定载重量为x吨，1辆小货车的额定载重量为y吨，

    根据题意1辆大货车与3辆小货车额定载重量的总和为23吨，可列；根据题意2辆大货车与5辆小货车额定载重量的总和为41吨，可列，则可以列方程组为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线y1＝2x+2交x轴、y轴于点A、C，直线交x轴、y轴于点B、C，点P(m，1)是△ABC内部(包括边上)的一点，则m的最大值与最小值之差为(　　)

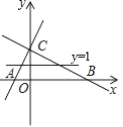
    A.2B.2.5C.3D.3.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有这样一个问题：探究函数的图象与性质.小彤根据学习函数的经验，对函数的图象与性质进行了探究.下面是小彤探究的过程，请补充完整：

    x

    -4

    -3.5

    -3

    -2

    -1

    0

    1

    2

    3

    3.5

    4

    y

    0

    m

    （1）求m的值为 ；

    （2）如图，在平面直角坐标系x0y 中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；

    （3）方程实数根的个数为 ；

    （4）观察图象，写出该函数的一条性质 ；

    （5）在第（2）问的平面直角坐标系中画出直线，根据图象写出方程的一个正数根约为 （精确到0.1）.

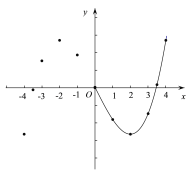
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y＝﹣x2+bx+c的图象经过点A（4，0），B（﹣4，﹣4），且与y轴交于点C．

    （1）求此二次函数的解析式；

    （2）证明：AO平分∠BAC；

    （3）在二次函数对称轴上是否存在一点P使得AP＝BP？若存在，请求出点P的坐标；若不存在，请说明理由．

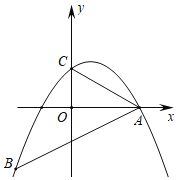
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果零售商店，通过对市场行情的调查，了解到两种水果销路比较好，一种是冰糖橙，一种是睡美人西瓜．通过两次订货购进情况分析发现，买40箱冰糖橙和15箱睡美人西瓜花去2000元，买20箱冰糖橙和30箱睡美人西瓜花去1900元．

    （1）请求出购进这两种水果每箱的价格是多少元？

    （2）该水果零售商在五一期间共购进了这两种水果200箱，冰糖橙每箱以40元价格出售，西瓜以每箱50元的价格出售，获得的利润为w元．设购进的冰糖橙箱数为a箱，求w关于a的函数关系式；

    （3）在条件（2）的销售情况下，但是每种水果进货箱数不少于30箱，西瓜的箱数不少于冰糖橙箱数的5倍，请你设计进货方案，并计算出该水果零售商店能获得的最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某年级共有150名女生，为了解该年级女生实心球成绩（单位：米）和一分钟仰卧起坐成绩（单位：个）的情况，从中随机抽取30名女生进行测试，获得了他们的相关成绩，并对数据进行整理、描述和分析．下面给出了部分信息．

    a. 实心球成绩的频数分布表如下：

    分组

    频数

    2

    m

    10

    6

    2

    1

    b. 实心球成绩在这一组的是：

    a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3

    c. 一分钟仰卧起坐成绩如下图所示：

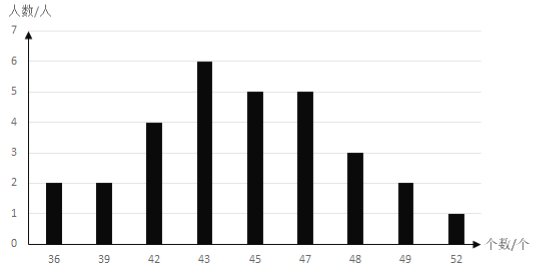
    根据以上信息，回答下列问题：

    （1） ①表中m的值为__________；

    ②一分钟仰卧起坐成绩的中位数为__________；

    （2）若实心球成绩达到7.2米及以上时，成绩记为优秀．

    ①请估计全年级女生实心球成绩达到优秀的人数；

    ②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下：

    女生代码

    A

    B

    C

    D

    E

    F

    G

    H

    实心球

    8.1

    7.7

    7.5

    7.5

    7.3

    7.2

    7.0

    6.5

    一分钟仰卧起坐

    *

    42

    47

    *

    47

    52

    *

    49

    其中有3名女生的一分钟仰卧起坐成绩未抄录完整，但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀，于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀，你同意体育委员的说法吗？并说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A、F、C、D四点在同一条直线上，AF=CD，AB∥DE，且AB=DE．

    （1）求证：△ABC≌△DEF；

    （2）若EF=3，DE=4，∠DEF=90°，请直接写出使四边形EFBC为菱形时AF的长度．

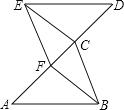
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AC平分∠BCD，AC⊥AB，E是BC的中点，AD⊥AE．

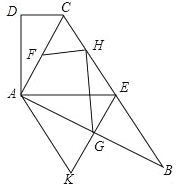
    （1）求证：AC2=CD·BC；

    （2）过E作EG⊥AB，并延长EG至点K，使EK=EB．

    ①若点H是点D关于AC的对称点，点F为AC的中点，求证：FH⊥GH；

    ②若∠B=30°，求证：四边形AKEC是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线y＝﹣2x+5分别与x轴，y轴交于点C、D，与反比例函数y＝的图象交于点A、B．过点A作AE⊥y轴于点E，过点B作BF⊥x轴于点F，连结EF；下列结论：①AD＝BC；②EF∥AB；③四边形AEFC是平行四边形；④S△EOF：S△DOC＝3：5．其中正确的个数是(　　)

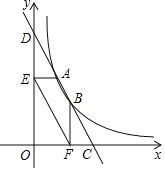
    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    同步练习册答案