
| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 当x=1时,y有最大值为-2 |
分析 根据b2-4ac的值决定抛物线与x轴的交点个数对A进行判断;根据二次函数的性质对B进行判断;通过计算自变量为0时的函数值可对C进行判断;把抛物线解析式配成顶点式可对D进行判断.
解答 解:A、△=22-4×(-1)×(-3)=-8<0,则抛物线与x轴没有交点,所以A选项错误;
B、a=-1<0,抛物线开口向下,所以B选项错误;
C、抛物线与y轴的交点坐标为(0,-3),所以C选项错误;
D、y=-(x-1)2-2,抛物线顶点坐标为(1,-2),所以当x=1时,y有最大值为-2,D选项错正确.
故选:D.
点评 本题考查了二次函数的性质,掌握开口方向,对称轴、顶点坐标以及与x轴的交点坐标的求法是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
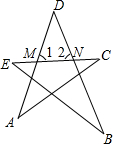 如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?
如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com