Question

16．如图所示，各边都相等的五边形ABCDE中，∠ABC=2∠DBE，求∠ABC．

Answer 1

分析 先根据等腰三角形的底角相等，得出∠AED+∠CDE=180°，判定AE∥CD，再根据一个角是60°的等腰三角形是等边三角形，得出∠ABC的度数．

解答 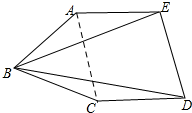证明：连接AC，
∵AE=AB，
∴∠ABE=∠AEB，同理∠CBD=∠CDB．
∵∠ABC=2∠DBE，
∴∠ABE+∠CBD=∠DBE，
∵∠ABE=∠AEB，∠CBD=∠CDB，
∴∠AEB+∠CDB=∠DBE，
∴∠AED+∠CDE=180°，
∴AE∥CD，
∵AE=CD，
∴四边形AEDC为平行四边形．
∴DE=AC=AB=BC．
∴△ABC是等边三角形，
∴∠ABC=60°

点评 本题主要考查等腰三角形的性质：等腰三角形的底角相等，以及等边三角形的判定定理．解题时注意，同旁内角互补，两直线平行．