
����Ŀ��������̽����
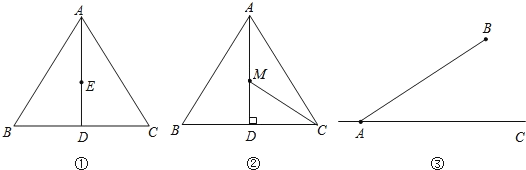
(1)��ͼ�٣���E������ABC��AD�ϵ�һ����,����AB����һ��F��ʹEF=![]() AE����˵�����ɣ�
AE����˵�����ɣ�
(2)��ͼ�ڣ���M�DZ߳�Ϊ2������ABC��AD�ϵ�һ���㣬��![]() AM+MC����Сֵ��
AM+MC����Сֵ��
����������
(3)��ͼ�ۣ�A��B�������600km,AC�DZ�ֱ���ض������������������һ����·����B��AC����̾���Ϊ360km����ƻ�����·��AC����һ����תվM������BM����һ����ֱ�Ĺ�·�����ͬ����������ÿǧ��·�ϵ��˷�����·�ϵ���������ô��Ϊʹͨ����·��A��M��ͨ����·��M��B�����˷Ѵﵽ��Сֵ����ȷ����תվM��λ��,�����AM�ij���(�����������)
���𰸡���1�������������2��![]() ����3��AM=(480
����3��AM=(480![]() )km��
)km��
��������
��1�����ݵȱ������ε����ʵó���BAD=30�����ó�EF=![]() AE��
AE��
��2����������ó�C��M��N��һ��ֱ����ʱ����ʱ![]() AM+MC��С������������ɣ�
AM+MC��С������������ɣ�
��3����BD��AC������Ϊ��D����AC���ڵ�B��һ������CAN=30������BF��AN������Ϊ��F����AC�ڵ�M����M��Ϊ������Rt��ABD�У����AD�ij�����Rt��MBD�У��ó�MD�ij������ɵó��𰸣�
�⣺(1)��ͼ������EF��AB������Ϊ��F����F��Ϊ����
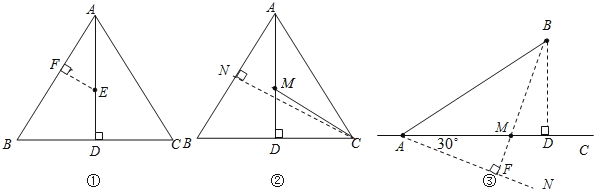
�������£��ߵ�E������ABC��AD�ϵ�һ���㣬
���BAD=30��
��EF��AB��
��EF=![]() AE��
AE��
(2)��ͼ��,��CN��AB,����Ϊ��N,��AD�ڵ�M,��ʱ![]() AM+MC��С����СΪCN�ij���
AM+MC��С����СΪCN�ij���
�ߡ�ABC�DZ߳�Ϊ2������ABC��
��CN=BCsin60=2��![]() =
=![]()
��MN+CM=12AM+MC=![]()
��![]() AM+MC����СֵΪ
AM+MC����СֵΪ![]()
(3)��ͼ��,��BD��AC,����Ϊ��D,��AC���ڵ�B��һ������CAN=30![]()
��BF��AN������Ϊ��F����AC�ڵ�M����M��Ϊ����
��Rt��ABD��,AD=![]() (km)
(km)
��Rt��MBD��,��MBD=��MAF=30,��MD=BDtan30=![]() (km)��
(km)��
����AM=(480![]() )km��
)km��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
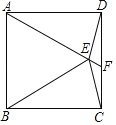
����Ŀ����ͼ����������ABCD�У���ABEΪ�ȱ������Σ�����DE��CE���ӳ�AE��CD��F�㣬���DEF�Ķ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ��
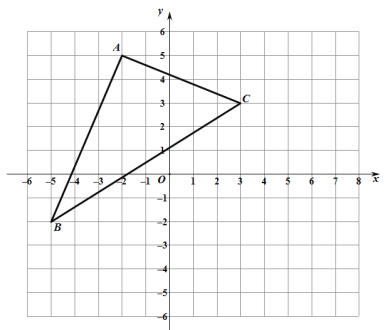
��1����д����ABC��������ꣻ
��2�������ABC�������
��3����ͼ����������ABC����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ���Ӧ��������A1B1C1����д����A1��B1��C1������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ɻ���һ���߶�����ˮƽֱ�߷��У����ڵ�![]() �������ǰ��С��
�������ǰ��С��![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ������С�������������
�������������������![]()
![]() ����
����![]() ��������С������������ʱ���С���ĸ���Ϊ
��������С������������ʱ���С���ĸ���Ϊ![]() �����С���߶Ⱥ��Բ��ƣ���ɻ����еĸ߶ȣ�����������ţ���
�����С���߶Ⱥ��Բ��ƣ���ɻ����еĸ߶ȣ�����������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ3����BAD��60������E��F�ڶԽ���AC�ϣ���E�ڵ�F����ࣩ����EF��1����DE+BF��СֵΪ_____
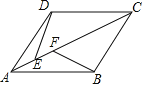
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ABΪ��O��ֱ����CDΪ�ң���CD��AB������ΪH��
��1�������O�İ뾶Ϊ4��CD=![]() ������BAC�Ķ�����
������BAC�Ķ�����
��2������EΪ��ADB���е㣬����OE��CE����֤��CEƽ����OCD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+bx+3��a��0����x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C�������ߵĶ���E����1��4�����Գ��ύx���ڵ�F��
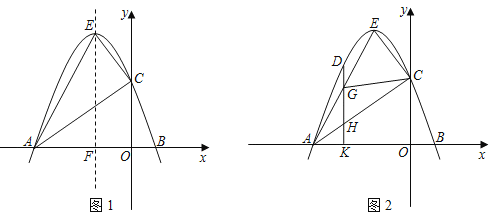
��1����ֱ��д�����������ߺ�ֱ��AE��ֱ��AC�Ľ���ʽ��
��2������AC��AE��CE���жϡ�ACE����״����˵�����ɣ�
��3����ͼ2����D����������һ���㣬���ĺ�����Ϊm���ҩ�3��m����1������D��DK��x���ڵ�K��DK�ֱ��߶�AE��AC�ڵ�G��H���ڵ�D���˶������У�
��DG��GH��HK�������߶��ܷ���ȣ�����ȣ��������D�����ꣻ������ȣ���˵�����ɣ�
���ڢٵ������£��ж�CG��AE��������ϵ����ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥![]() ����ǰ����һб��
����ǰ����һб��![]() �ף��½�
�ף��½�![]() ��С����б���µĵ�
��С����б���µĵ�![]() �����¥��
�����¥��![]() ������Ϊ
������Ϊ![]() ��б���ϵĵ�
��б���ϵĵ�![]() �����¥��
�����¥��![]() ������
������![]() Ϊ���е�
Ϊ���е�![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�
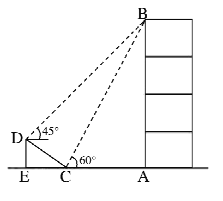
��1����б��![]() �ĸ߶�
�ĸ߶�![]() ��
��
��2�����¥![]() �ĸ߶�(�����������)
�ĸ߶�(�����������)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com