
 如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.
如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$. 分析 连接AC、F1E1、DE1,F1E1交AD于M,延长BE1交DF1于H,如图,先利用正方形的性质得到∠DAC=∠BAC=45°,再根据旋转的性质得∠E1AE=∠FAF1=45°,AE1=AF1=AE=AF=1,于是可判断点E1在AC上,△AE1F1为等腰直角三角形,再证明E1F1∥AB,作E1N⊥AB于N,计算出BE1=$\sqrt{5}$,易证得△ABE1≌△ADE1≌△ADF1得到DE1=DF1=BE1=$\sqrt{5}$,∠ABH=∠ADH,接着利用面积法计算出E1H=$\frac{3\sqrt{5}}{5}$,然后计算出HF1=$\frac{\sqrt{5}}{5}$,所以DH=DF1-HF1=$\frac{4\sqrt{5}}{5}$.
解答 解:连接AC、F1E1、DE1,F1E1交AD于M,延长BE1交DF1于H,如图,
∵四边形ABCD为正方形,
∴∠DAC=∠BAC=45°,
∵△AEF绕点A逆时针旋转45°,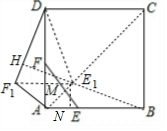
∴∠E1AE=∠FAF1=45°,AE1=AF1=AE=AF=1,
∴点E1在AC上,△AE1F1为等腰直角三角形,
∴∠AE1F1=45°,E1F1=$\sqrt{2}$,AM=$\frac{\sqrt{2}}{2}$,
∴E1F1∥AB,DM=$\frac{3\sqrt{2}}{2}$,
作E1N⊥AB于N,如图,AN=E1N=$\frac{\sqrt{2}}{2}$,
∴BE=AB-AN=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$,
∴BE1=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{5}$,
易证得△ABE1≌△ADE1≌△ADF1,
∴DE1=DF1=BE1=$\sqrt{5}$,∠ABH=∠ADH,
∴∠DHB=∠DAB=90°,
∵$\frac{1}{2}$DM•E1F1=$\frac{1}{2}$•E1H•DF1,
∴E1H=$\frac{\sqrt{2}×\frac{3\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$,
在Rt△HF1E1中,HF1=$\sqrt{(\sqrt{2})^{2}-(\frac{3\sqrt{5}}{5})^{2}}$=$\frac{\sqrt{5}}{5}$,
∴DH=DF1-HF1=$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{4\sqrt{5}}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和正方形的性质.


科目:初中数学 来源: 题型:填空题
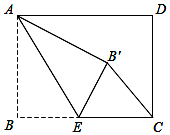 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,CB′的长为2或$\sqrt{10}$.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,CB′的长为2或$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
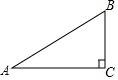 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 21 | B. | 103 | C. | 116 | D. | 121 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
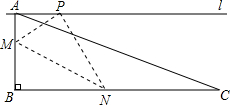 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )| A. |  | B. | 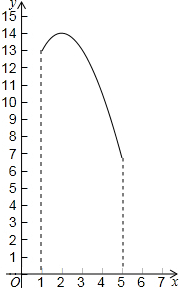 | ||
| C. | 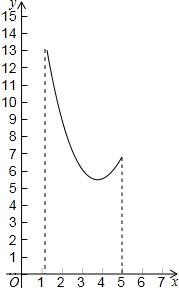 | D. | 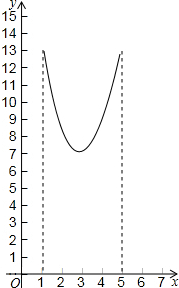 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
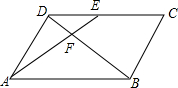 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
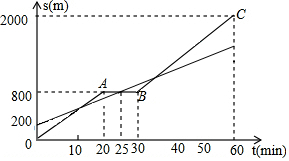 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com