
【题目】已知二次函数y=ax2﹣(2a+1)x+c(a>0)的图象经过坐标原点O,一次函数y=﹣x+4与x轴、y轴分别交于点A、B.
(1)c= ,点A的坐标为 ;
(2)若二次函数y=ax2﹣(2a+1)x+c的图象经过点A,求a的值;
(3)若二次函数y=ax2﹣(2a+1)x+c的图象与△AOB只有一个公共点,直接写出a的取值范围.
【答案】(1)c=0,点 A 的坐标为(4,0);(2)a=0.5;(3)a 的取值范围是![]() .
.
【解析】
(1)根据题意和题目中的函数解析式可以求得c的值和点A的坐标;
(2)根据(1)中点A得坐标和二次函数y=ax2-(2a+1)x+c的图象经过点A,可以求得a的值;
(3)根据题意可以求得点B的坐标,然后根据二次函数与x轴的两个交点坐标为(0,0)和(![]() ,0),二次函数y=ax2-(2a+1)x+c的图象与△AOB只有一个公共点,可以求得a的取值范围.
,0),二次函数y=ax2-(2a+1)x+c的图象与△AOB只有一个公共点,可以求得a的取值范围.
(1)∵二次函数 y=ax2﹣(2a+1)x+c(a>0)的图象经过坐标原点 O,
∴当 x=0 时,c=0,
将 y=0 代入 y=﹣x+4,得 x=4,即点 A 的坐标为(4,0);
(2)∵二次函数 y=ax2﹣(2a+1)x+c 的图象经过点 A,点 A 的坐标为(4,0),
∴0=a×42﹣(2a+1)×4,
解得,a=0.5;
(3)将 x=0 代入 y=﹣x+4,得 y=4,即点 B 的坐标为(0,4),
∵点 A(4,0),点 O 的坐标为(0,0),二次函数 y=ax2﹣(2a+1)x 的图象与
△AOB 只有一个公共点,
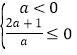 ,
,
解得,-![]() ≤a<0.
≤a<0.
即 a 的取值范围是,-![]() ≤a<0.
≤a<0.


科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则有以下四个结论:①
,则有以下四个结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() 的周长是10;④
的周长是10;④![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
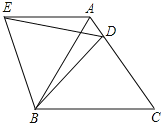
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)
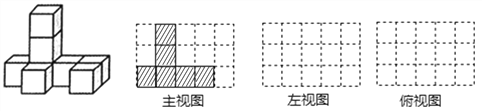
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,![]() ,
,![]() ,等腰
,等腰![]() 的顶点
的顶点![]() 在第二象限,
在第二象限,![]() 交
交![]() 轴于点
轴于点![]() .
.
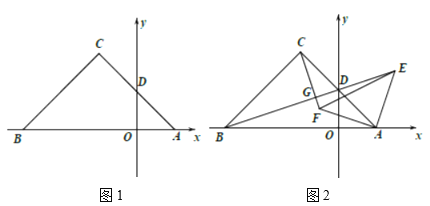
(1)如图1,求证![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,若点
的延长线上,若点![]() 坐标为
坐标为![]() ,以
,以![]() 为直角边在左侧作等腰
为直角边在左侧作等腰![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
①求点![]() 的坐标;
的坐标;
②求证![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
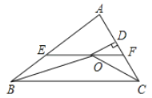
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,下列四个结论:
,下列四个结论:
①![]() ;②
;②![]() ;
;
③点![]() 到
到![]() 各边的距离相等;③设
各边的距离相等;③设![]() ,
,![]() ,则
,则![]() .
.
其中正确的结论是__________.(填所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com