
分析 (1)由题意得:y=$\frac{1}{2}$•x•(22-x)=-$\frac{1}{2}$x2+11x(0<x<22),当y=48,解方程即可解决问题.
(2)利用配方法,根据二次函数的性质即可解决问题.
(3)如图,作AD⊥BC于D,设BD=x,则CD=11-x,因为△ABC的周长=BC+AB+AC=11+$\sqrt{1{1}^{2}+{x}^{2}}$+$\sqrt{1{1}^{2}+(11-x)^{2}}$,欲求△△ABC的周长最小值,即就是求$\sqrt{1{1}^{2}+{x}^{2}}$+$\sqrt{1{1}^{2}+(11-x)^{2}}$的最小值,相当于在x轴上找一点M(x,0),到E(0,11),F(11,11)的距离之和的最小值,作点E关于x轴的对称点E′,连接FE′交x则于M,此时ME+MF最小,最小值=$\sqrt{1{1}^{2}+2{2}^{2}}$=11$\sqrt{5}$,由此即可解决问题.
解答 解:(1)由题意得:y=$\frac{1}{2}$•x•(22-x)=-$\frac{1}{2}$x2+11x(0<x<22),
当y=48时,-$\frac{1}{2}$x2+11x=48,解得x=6或16,
当△ABC面积为48时BC的长为6 或16;
(2)由(1)得:,y=-$\frac{1}{2}$x2+11x=-$\frac{1}{2}$(x-11)2+$\frac{121}{2}$,
∴当x=11即BC=11时,△ABC的面积最大,最大面积是$\frac{121}{2}$;
(3)△ABC的周长存在最小的情形,理由如下:
如图,作AD⊥BC于D,设BD=x,则CD=11-x,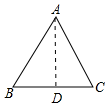
∵△ABC的周长=BC+AB+AC=11+$\sqrt{1{1}^{2}+{x}^{2}}$+$\sqrt{1{1}^{2}+(11-x)^{2}}$,
欲求△△ABC的周长最小值,即就是求$\sqrt{1{1}^{2}+{x}^{2}}$+$\sqrt{1{1}^{2}+(11-x)^{2}}$的最小值,
相当于在x轴上找一点M(x,0),到E(0,11),F(11,11)的距离之和的最小值,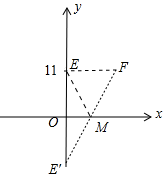
作点E关于x轴的对称点E′,连接FE′交x则于M,此时ME+MF最小,最小值=$\sqrt{1{1}^{2}+2{2}^{2}}$=11$\sqrt{5}$
当△ABC面积最大时,存在其周长最小的情形,最小周长为11$\sqrt{5}$+11.
点评 本题考查二次函数的应用、三角形的面积、周长、两点之间线段最短等知识,解题的关键是学会用转化的思想思考问题,本题的突破点是把求$\sqrt{1{1}^{2}+{x}^{2}}$+$\sqrt{1{1}^{2}+(11-x)^{2}}$的最小值问题,转化为在x轴上找一点M(x,0),到E(0,11),F(11,11)的距离之和的最小值,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 96a-8a2 | B. | 8a2-96a | C. | 98a-6a2 | D. | 6a2-98a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
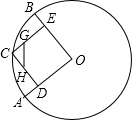 在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )
在⊙O中,半径OA、OB互相垂直,点C为弧$\widehat{AB}$上一点(不与A、B重合),CD⊥OA,CE⊥OB,垂足分别为D、E.点G、H分别在CE、CD上,且CG=$\frac{1}{3}$CE,CH=$\frac{1}{3}$CD,当C点在弧$\widehat{AB}$上运动时,GH的长度( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.
如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
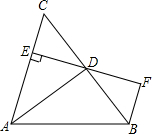 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
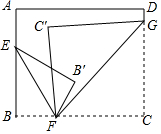 如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.
如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com