
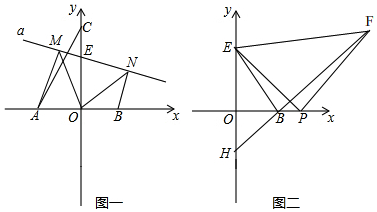
分析 (1)先根据△OMN是以MN为斜边的等腰直角三角形,以及AM⊥MN,判定△AOM≌△EON(ASA),得出AO=EO,再根据含30度角的直角三角形的性质,求得AO=$\frac{1}{2}$AC=3,进而得出EO=3,即可得到E(0,3);
(2)先过点F作FG⊥x轴于G,则∠PGF=∠EOP=90°,根据△EFP是等腰直角三角形,判定△OPE≌△GFP(AAS),得出OP=GF,OE=GP,再根据OE=OB=3,得出GF=GB,进而得到△BOH是等腰直角三角形,可得OB=OH=3,据此求得H(0,-3).
解答 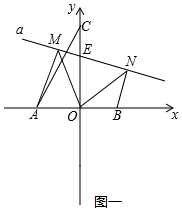 解:(1)如图1,∵△OMN是以MN为斜边的等腰直角三角形,
解:(1)如图1,∵△OMN是以MN为斜边的等腰直角三角形,
∴∠MNO=∠NMO=45°,MO=NO,
∵AM⊥MN,
∴∠AMO=45°,
∴∠AMO=∠ENO,
∵∠MON=∠AOE=90°,
∴∠AOM=∠EON,
在△AOM和△EON中,
$\left\{\begin{array}{l}{∠AMO=∠ENO}\\{MO=NO}\\{∠AOM=∠EON}\end{array}\right.$,
∴△AOM≌△EON(ASA),
∴AO=EO,
∵AC=6,且∠ACO=30°,
∴Rt△AOC中,AO=$\frac{1}{2}$AC=3,
∴EO=3,
即E(0,3);
(2)如图2,过点F作FG⊥x轴于G,则∠PGF=∠EOP=90°,
∵△EFP是等腰直角三角形,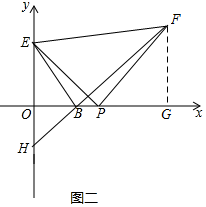
∴PE=FP,∠EPF=90°,
∴∠OPE+∠GPF=90°=∠GFP+∠GPF,
∴∠OPE=∠GFP,
在△OPE和△GFP中,
$\left\{\begin{array}{l}{∠PGF=∠EOP}\\{∠OPE=∠GFP}\\{PE=FP}\end{array}\right.$,
∴△OPE≌△GFP(AAS),
∴OP=GF,OE=GP,
∴OG=OP+GP=GF+OE,
又∵OG=OB+BG,
∴GF+OE=OB+BG,
∵B是A点关于y轴的对称点,AO=3,OE=3,
∴OE=OB=3,
∴GF=GB,
∴∠GBF=45°=∠OBH,
又∵∠BOH=90°,
∴△BOH是等腰直角三角形,
∴OB=OH=3,
∴H(0,-3).
点评 本题属于三角形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定与性质以及含30°角的直角三角形,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行求解.解题时注意:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.


科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
如图所示,用量角器度量一些角的度数。下列结论中正确的是( )
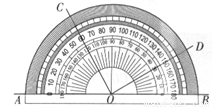
A. ∠BOC=60° B. ∠COD=150°
C. ∠AOC与∠BOD的大小相等 D. ∠AOC与∠BOD互余
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
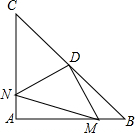 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.
如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com