
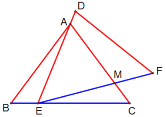
【题目】如图,![]() (点
(点![]() ,
,![]() 分别与点
分别与点![]() ,
,![]() 对应),
对应),![]() ,
,![]() .
.![]() 固定不动,
固定不动,![]() 运动,并满足点
运动,并满足点![]() 在
在![]() 边从
边从![]() 向
向![]() 移动(点
移动(点![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 始终经过点
始终经过点![]() ,
,![]() 与
与![]() 边交于点
边交于点![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() ______.
______.
【答案】![]() 或
或 ![]()
【解析】
首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案.
解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,
∵∠AEB=∠MAE+∠C,∠EMC=∠MAE+∠AEM=∠MAE+∠B=∠MAE+∠C
∴∠AEB=∠EMC
又∵∠B=∠C
∴△ABE≌△ECM,
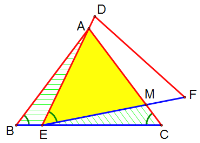
∴CE=AB=5,
∴BE=BC-EC=6-5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴![]()
∴![]()
∴![]() .
.
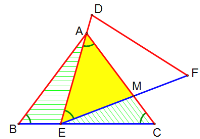
故答案为:![]() 或
或 ![]() .
.


科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,已知线段![]() ,现要在该网格内再确定格点
,现要在该网格内再确定格点![]() 和格点
和格点![]() ,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )
,某数学探究小组在探究时发现以下结论:以下结论不正确的是( )

A.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为正方形的有2种;
为正方形的有2种;
B.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为菱形的(正方形除外)有3种;
为菱形的(正方形除外)有3种;
C.将线段![]() 平移得到线段
平移得到线段![]() ,使四边形
,使四边形![]() 为矩形的(正方形除外)有两种;
为矩形的(正方形除外)有两种;
D.不存在以![]() 为对角线的四边形
为对角线的四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(Ⅰ)根据题意填表:

(Ⅱ)设方案①应缴水费为![]() 元,方案②应缴水费为
元,方案②应缴水费为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)当![]() 时,通过计算说明居民选择哪种付费方式更合算.
时,通过计算说明居民选择哪种付费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从机械厂购进甲、乙两种零件进行销售,若甲种零件每件的进价是乙种零件每件进价的![]() ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
(1)求每件甲种零件和每件乙种零件的进价分别为多少元?
(2)若该商店计划购进甲、乙两种零件共110件,准备将零件批发给零售商. 甲种零件的批发价是每件100元,乙种零件的批发价是每件130元,该商店计划将这批产品全部售出从零售商处获利不低于3000元,那么该商店最多购进多少件甲种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系 ![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
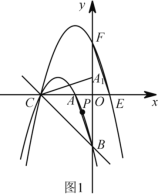
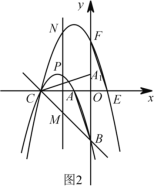
(1)求抛物线![]() 的解析式.
的解析式.
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若 ![]() ,求
,求![]() 点的坐标;
点的坐标;
②如图![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.
(1)求证:AB=AC;
(2)若AB=4,⊙O的半径为![]() ,求PD的长.
,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
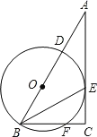
【题目】在 Rt△ABC 中,∠ACB=90°,BE 平分∠ABC,D 是边 AB 上一点,以 BD为直径的⊙O 经过点 E,且交 BC 于点 F.
(1)求证:AC 是⊙O 的切线;
(2)若 BC=8,⊙O 的半径为 5,求 CE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com