
如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=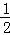 ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(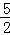 ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
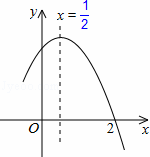
A. ①②④ B③④ C.①③④ D. ①②
科目:初中数学 来源: 题型:
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )

A. 15° B.30° C.45° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为
查看答案和解析>>
科目:初中数学 来源: 题型:
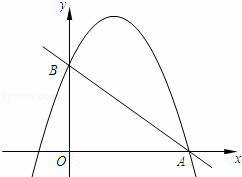
如图,在平面直角坐标系xOy中,点A坐标为(8,0),点B在y轴的正半轴上,且cot∠OAB= ,抛物线y=﹣
,抛物线y=﹣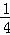 x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求b、c的值;
(2)过点B作CB⊥OB,交这个抛物线于点C,以点C为圆心,CB为半径长的圆记作圆C,以点A为圆心,r为半径长的圆记作圆A.若圆C与圆A外切,求r的值;
(3)若点D在这个抛物线上,△AOB的面积是△OBD面积的8倍,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是( )
A. y=x2﹣1 B.y=x2+1 C.y=(x﹣1)2 D. y=(x+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ,
, ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )
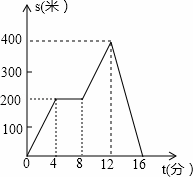
A. 小明看报用时8分钟 B. 公共阅报栏距小明家200米
C. 小明离家最远的距离为400米 D. 小明从出发到回家共用时16分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com