
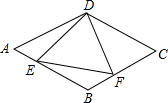
 如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:
如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:分析 连接BD,由菱形的性质可证明△ADE≌△BDF,得出DE=DF,再证出∠EDF=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△DEF是等边三角形,从而判断①正确;根据已知条件不能得出∠CDF=2∠ADE,从而判断②错误;过点D作DM⊥AB于M,根据等腰三角形三线合一的性质得出AM=$\frac{1}{2}$AB=3.在Rt△ADM中,利用勾股定理求出DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=3$\sqrt{3}$,则四边形DEBF的面积=△ABD的面积=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,从而判断③正确;若AE=$\frac{1}{3}$AB,可知BF=2,在Rt△EDM中,利用勾股定理求出DE=$\sqrt{E{M}^{2}+D{M}^{2}}$=$\sqrt{{1}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$,从而判断④正确.
解答  解:连结BD.
解:连结BD.
∵在菱形ABCD中,AB=6,∠A=60°,
∴AB=AD=BC=CD=6,∠C=∠A=60°,
∴△ABD与△BCD都是等边三角形,
∴DA=DB,∠DAE=∠DBF=60°,又AE=BF,
∴△ADE≌△BDF,
∴DE=DF,∠ADE=∠BDF,
∴∠EDF=∠ADB=60°,
∴△DEF是等边三角形,①正确;
过点D作DM⊥AB于M,则AM=$\frac{1}{2}$AB=3.
在Rt△ADM中,DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∵△ADE≌△BDF,
∴四边形DEBF的面积=△ABD的面积=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,③正确;
若AE=$\frac{1}{3}$AB,可知BF=AE=2,
∴EM=1.
在Rt△EDM中,DE=$\sqrt{E{M}^{2}+D{M}^{2}}$=$\sqrt{{1}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$,④正确.
只有②是错误的.
故答案为①③④.
点评 本题考查了菱形的性质,等边三角形、全等三角形的判定与性质,等腰三角形的性质,勾股定理,三角形、四边形的面积,熟练掌握菱形的性质,通过作辅助线证明三角形全等是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.
现要建造一段铁路,其路基的横断面ABCD是等腰梯形,上底CD=8米,高DH为2.5米,坡度i=1:1.2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,
如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )
据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )| A. | 6.2×109 | B. | 6.2×108 | C. | 62×108 | D. | 0.62×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4<a≤-3 | B. | -4≤a<-3 | C. | -4≤a≤-3 | D. | -4<a<-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com