
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
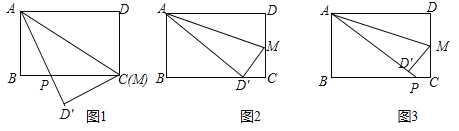
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
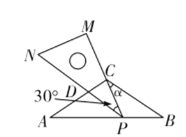
【题目】在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动.
已知,在等腰三角形纸片ABC中,CA=CB=5,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段BA上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= °,点P从B向A运动时,∠ADP逐渐变 (填“大”或“小”).
(2)合作交流
当AP等于多少时,△APD≌△BCP,请说明理由.
(3)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
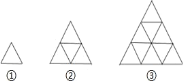
A. 63B. 60C. 56D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=![]() x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
(1)求b,c的值及D点的坐标;
(2)求点E在OC上运动时,四边形OEBF的面积有怎样的规律性?并证明你的结论;
(3)连接EF,BD,设OE=m,△BEF与△BED的面积之差为S,问:当m为何值时S最小,并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
已知在纸面上有一数轴(如图所示),
操作一:

(1)折叠纸面,使表示的点1与1表示的点重合,则2表示的点与___表示的点重合;
操作二:
(2)折叠纸面,使1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数___表示的点重合;
②![]() 表示的点与数___表示的点重合
表示的点与数___表示的点重合
若数轴上A. B两点之间距离为9,(A在B的左侧),且A. B两点经折叠后重合,求A. B两点表示的数是多少?
操作三:
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝国庆70华诞,近日某检修小组从A地出发,在东西走向的公路上检修路灯线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下(单位:km).

(1)收工时距A地的距离是 ;
(2)在第 次记录时距A地最远.这个距离是 km
(3)若每km耗油0.2升,问这七次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由若干个正方体形状的木块堆成的,平放于桌面上。其中,上面正方体的下底面的四个顶点恰是下面相邻正方体的上底面各边的中点,如果最下面的正方体的棱长为1.
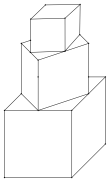
(1)当只有两个正方体放在一起时,这两个正方体露在外面的面积和是 ;
(2)当这些正方体露在外面的面积和超过![]() 时,那么正方体的个数至少是多少?
时,那么正方体的个数至少是多少?
(3)按此规律下去,这些正方体露在外面的面积会不会一直增大?如果会,请说明理由;如果不会,请求出不会超过哪个数值?(提示:所有正方体侧面面积加上所有正方体上面露出的面积之和,就是需求的面积,从简单入手,归纳规律.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
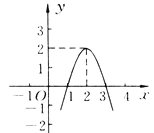
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com