
如图,已知抛物线y= x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
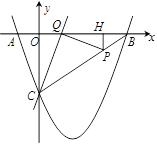
(-1,0),过点C的直线y= x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.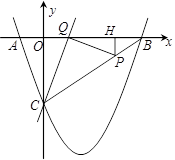
【小题1】(1)填空:点C的坐标是_ _,b=_ _;
【小题2】(2)求线段QH的长(用含t的式子表示);
【小题3】(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
【小题1】(1)(0,-3),b=-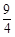 .
.
【小题2】(2)由(1),得y=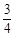 x2-
x2-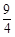 x-3,它与x轴交于A,B两点,得B(4,0).
x-3,它与x轴交于A,B两点,得B(4,0).
∴OB=4,又∵OC=3,∴BC=5.
由题意,得△BHP∽△BOC,
∵OC∶OB∶BC=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=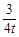 x-3与x轴交于点Q,得Q(4t,0).
x-3与x轴交于点Q,得Q(4t,0).
∴OQ=4t.
①当H在Q、B之间时,
QH=OH-OQ
=(4-4t)-4t=4-8t.··················································· 3分
②当H在O、Q之间时,
QH=OQ-OH
=4t-(4-4t)=8t-4.··················································· 4分
综合①,②得QH=|4-8t|;
【小题3】(3)存在t的值,使以P、H、Q为顶点的三角形与△COQ相似.
①当H在Q、B之间时,QH=4-8t,
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得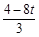 =
=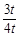 ,
,
∴t=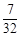 .········································································· 5分
.········································································· 5分
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得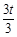 =
= ,
,
即t2+2t-1=0.
∴t1= -1,t2=-
-1,t2=- -1(舍去).······································· 6分
-1(舍去).······································· 6分
②当H在O、Q之间时,QH=8t-4.
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得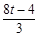 =
=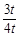 ,
,
∴t=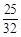 .········································································· 7分
.········································································· 7分
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得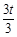 =
=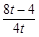 ,
,
即t2-2t+1=0.
∴t1=t2=1(舍去).····························································· 8分
综上所述,存在 的值,t1=
的值,t1= -1,t2=
-1,t2=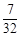 ,t3=
,t3=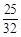 .
.
解析


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
如图,已知抛物线y=x![]() -ax+a
-ax+a![]() -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
(1)求a的值;
(2)当四边形ODPQ为矩形时,求这个矩形的面积;
(3)当四边形PQBC的面积等于14时,求t的值.
(4)当t为何值时,△PBQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年江苏省苏州市中考模拟数学卷 题型:解答题
(本题9分)如图,已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点,与y轴交于点C,且点C、D是抛物线上的一对对称点.
【小题1】(1)求抛物线的解析式;
【小题2】(2)求点D的坐标,并在图中画出直线BD;
【小题3】(3)求出直线BD的一次函数解析式,并根据图象回答:当x满足什么条件时,上述二次函数的值大于该一次函数的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年苏州工业园区九年级下学期学科调研数学卷 题型:解答题
(9分)如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.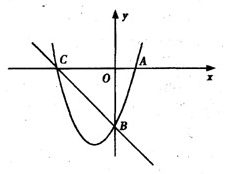
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,
求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形
为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年陕西省兴平市九年级上学期期末练习数学卷 题型:解答题
(本题满分10分)
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(—1,0)、C(0,—3)两点,与x轴交于另一点B.
1.(1)求这条抛物线所对应的函数关系式;
2.(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
3.(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com