

科目:初中数学 来源:不详 题型:解答题
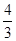 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
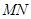 :
: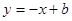 与
与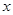 轴交于点
轴交于点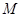 (4,0),与
(4,0),与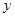 轴交于点
轴交于点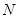 ,长方形
,长方形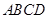 的边
的边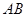 在
在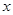 轴上,
轴上,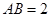 ,
,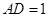 .长方形
.长方形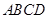 由点
由点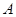 与点
与点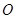 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿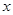 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点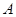 与点
与点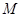 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为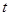 秒,长方形
秒,长方形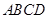 与△
与△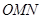 重合部分的面积为
重合部分的面积为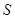 .
.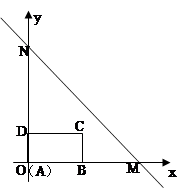
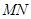 的解析式;
的解析式;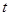 =1时,请判断点
=1时,请判断点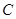 是否在直线
是否在直线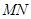 上,并说明理由;
上,并说明理由; 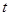 为何值时,点
为何值时,点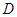 在直线
在直线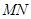 上;
上;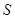 与
与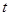 的函数关系式.
的函数关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
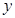 (元)与印制数量
(元)与印制数量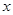 (份)之间的关系式;
(份)之间的关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ),过x轴上的点1、3、5、7、9、11……分别作x轴的垂线,与直线OP相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn则Sn关于n的函数关系式是____.
),过x轴上的点1、3、5、7、9、11……分别作x轴的垂线,与直线OP相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn则Sn关于n的函数关系式是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com