练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    某厂家生产的产品出厂时可以提供如图所示的三种方式进行打包．（其中a＞b＞c）

    （1）请用代数式分别表示出三种方式的绳子长度l1，l2，l3；
    （2）若出厂时只能采用一种方式统一进行打包，那么最节省打包所费绳子的方式为
    （2）
    （2）
    ．（填序号）
    分析：（1）方式一中有4a，2b和6c，方式二中有2a，4b和6c，方式三中有4a，4b和4c；
    （2）根据a＞b＞c比较三种打包方式的绳子长即可．
    解答：解：（1）方式（1）：l1=4a+2b+6c，
    方式（2）：l2=2a+4b+6c，
    方式（3）：l3=4a+4b+4c，

    （2）∵a＞b＞c，
    ∴2a+4b+6c＜4a+2b+6c，
    ∴方式一的绳子比方式二长；
    ∵a＞b＞c，
    ∴4a+4b+4c＞4a+2b+6c，
    ∴方式三的绳子比方式二长；
    ∴方式二的绳子最短，
    故选用方式（2）．
    故答案为：（2）．
    点评：本题考查了列代数式，以及比较大小，解题的关键是得出三种方式的绳子长．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2013届江苏无锡市大桥区九年级上学期期末考试数学试卷（带解析） 题型：解答题

    国内某企业生产一种隔热瓦（其厚度忽略不计），形状近似为正方形，边长x（cm）在5~25之间（包括5和25），每片隔热瓦的成本价（元）与它的面积（cm2）成正比例．出厂价P（元）与它的边长x（cm）满足一次函数，图象如图所示．

    （1）已知出厂一张边长为15cm的隔热瓦，获得的利润是55元（利润=出厂价-成本价）.
    ①求每片的隔热瓦利润Q（元）与边长x（cm）之间满足的函数关系式；
    ②当边长为多少时，出厂的隔热瓦能获得最大利润？最大利润是多少？
    （2）在（1）的基础上，如果厂家继续扩大产品规模，从5cm~25cm扩大到5cm~60cm．由于20cm~40cm的隔热瓦属于国家科技项目，国家对这部分产品进行贴补．每片隔热瓦贴补W（元）与它的边长x（cm）满足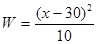：．在推广20cm~40cm的隔热瓦时，厂家进行市场营销，这种规格的隔热瓦广告费为每片10元．要使每片隔热瓦的利润不低于60.4元，求5cm~60cm的隔热瓦边长x的取值范围（x取整数）．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏无锡市大桥区九年级上学期期末考试数学试卷（解析版） 题型：解答题

    国内某企业生产一种隔热瓦（其厚度忽略不计），形状近似为正方形，边长x（cm）在5~25之间（包括5和25），每片隔热瓦的成本价（元）与它的面积（cm2）成正比例．出厂价P（元）与它的边长x（cm）满足一次函数，图象如图所示．

    （1）已知出厂一张边长为15cm的隔热瓦，获得的利润是55元（利润=出厂价-成本价）.

    ①求每片的隔热瓦利润Q（元）与边长x（cm）之间满足的函数关系式；

    ②当边长为多少时，出厂的隔热瓦能获得最大利润？最大利润是多少？

    （2）在（1）的基础上，如果厂家继续扩大产品规模，从5cm~25cm扩大到5cm~60cm．由于20cm~40cm的隔热瓦属于国家科技项目，国家对这部分产品进行贴补．每片隔热瓦贴补W（元）与它的边长x（cm）满足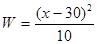：．在推广20cm~40cm的隔热瓦时，厂家进行市场营销，这种规格的隔热瓦广告费为每片10元．要使每片隔热瓦的利润不低于60.4元，求5cm~60cm的隔热瓦边长x的取值范围（x取整数）．

     

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    某厂家生产的产品出厂时可以提供如图所示的三种方式进行打包．（其中a＞b＞c）

    精英家教网

    （1）请用代数式分别表示出三种方式的绳子长度l1，l2，l3；
    （2）若出厂时只能采用一种方式统一进行打包，那么最节省打包所费绳子的方式为______．（填序号）

    查看答案和解析>>

    同步练习册答案