
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
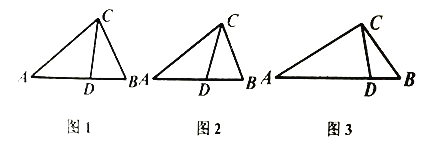
![]() 如图1,在
如图1,在![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() , 则
, 则![]() 的度数是
的度数是
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,求证:
,求证: ![]() 为
为![]() 的完美分割线.
的完美分割线.
![]() 如图2,
如图2,![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,我们将函数![]() 的图象绕原点
的图象绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到的新曲线
后得到的新曲线![]() 称为“逆旋抛物线”.
称为“逆旋抛物线”.
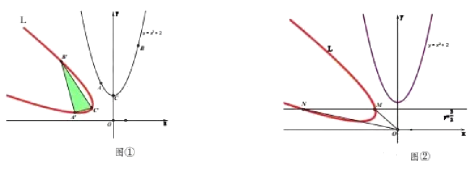
(1)如图①,己知点![]() ,
,![]() 在函数
在函数![]() 的图象上,抛物线的顶点为
的图象上,抛物线的顶点为![]() ,若
,若![]() 上三点
上三点![]() 、
、![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 旋转后的对应点,连结
旋转后的对应点,连结![]() ,
,![]() 、
、![]() ,则
,则![]() __________;
__________;
(2)如图②,逆旋抛物线![]() 与直线
与直线![]() 相交于点
相交于点![]() 、
、![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
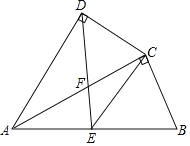
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD.
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
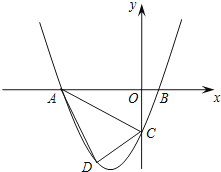
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
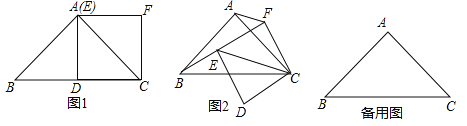
【题目】(1)问题发现
如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 恰好与点
恰好与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 的数量关系为______________;
的数量关系为______________;
(2)拓展探究
在(1)的条件下,如果正方形![]() 绕点
绕点![]() 旋转,连接
旋转,连接![]() ,线段
,线段![]() 与
与![]() 的数量关系有无变化?请仅就图2的情形进行说明;
的数量关系有无变化?请仅就图2的情形进行说明;
(3)问题解决.
当正方形![]() 旋转到
旋转到![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
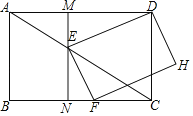
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且![]() =k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
(1)求证:△MED∽△NFE;
(2)当EF=FC时,求k的值.
(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,某风景区推出两种旅游观光活动付费方式:若人数不超过20人,人均缴费500元;若人数超过20人,则每增加一位旅客,人均收费降低10元,但是人均收费不低于350元.现在某单位在国庆期间组织一批贡献突出的职工到该景区旅游观光,支付了12000元观光费,请问:该单位一共组织了多少位职工参加旅游观光活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
两点.![]() 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为_____________.
的坐标为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com