
 如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.分析 (1)利用圆内接四边形对角互补以及邻补角的定义得出∠FED=∠A,进而得出∠B+∠A=90°,求出答案;
(2)利用相似三角形的判定与性质首先得出△FED∽△FAC,进而求出即可.
解答 (1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC=180°,
∴∠FED=∠A,
∵∠B+∠FED=90°,
∴∠B+∠A=90°,
∴∠BCA=90°,
∴BC是⊙O的切线;
(2)解:∵∠CFA=∠DFE,∠FED=∠A,
∴△FED∽△FAC,
∴$\frac{DF}{FC}$=$\frac{DE}{AC}$,
∴$\frac{2}{6}$=$\frac{3}{AC}$,
解得:AC=9,即⊙O的直径为9.
点评 此题主要考查了相似三角形的判定与性质以及切线的判定等知识,得出△FED∽△FAC是解题关键.


科目:初中数学 来源: 题型:解答题
 为了学生的终身发展,某中学积极开展第二课堂,下面是该中学一部分学生参加五个学习小组的统计表和扇形统计图,请根据图表提供的信息回答下列问题:
为了学生的终身发展,某中学积极开展第二课堂,下面是该中学一部分学生参加五个学习小组的统计表和扇形统计图,请根据图表提供的信息回答下列问题:| 学习小组 | 体育 | 美术 | 音乐 | 写作 | 奥数 |
| 人数 | 75 | 75 | 54 | 30 | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. | 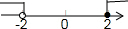 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
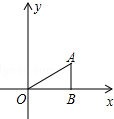 如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
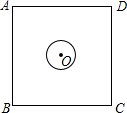 如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$.
如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com