
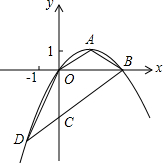
 如图,顶点为A($\sqrt{3}$,1)的抛物线经过坐标原点O,与x轴交于点B.
如图,顶点为A($\sqrt{3}$,1)的抛物线经过坐标原点O,与x轴交于点B.分析 (1)用待定系数法求出抛物线解析式,
(2)先求出直线OA对应的一次函数的表达式为y=$\frac{\sqrt{3}}{3}$x.再求出直线BD的表达式为y=$\frac{\sqrt{3}}{3}$x-2.最后求出交点坐标C,D即可;
(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
解答 解:(1)∵抛物线顶点为A($\sqrt{3}$,1),
设抛物线解析式为y=a(x-$\sqrt{3}$)2+1,
将原点坐标(0,0)在抛物线上,
∴0=a($\sqrt{3}$)2+1
∴a=-$\frac{1}{3}$.
∴抛物线的表达式为:y=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x.
(2)令y=0,得 0=-$\frac{1}{3}$x2+$\frac{2\sqrt{3}}{3}$x,
∴x=0(舍),或x=2$\sqrt{3}$
∴B点坐标为:(2$\sqrt{3}$,0),
设直线OA的表达式为y=kx,
∵A($\sqrt{3}$,1)在直线OA上,
∴$\sqrt{3}$k=1,
∴k=$\frac{\sqrt{3}}{3}$,
∴直线OA对应的一次函数的表达式为y=$\frac{\sqrt{3}}{3}$x.
∵BD∥AO,
设直线BD对应的一次函数的表达式为y=$\frac{\sqrt{3}}{3}$x+b,
∵B(2$\sqrt{3}$,0)在直线BD上,
∴0=$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$+b,
∴b=-2,
∴直线BD的表达式为y=$\frac{\sqrt{3}}{3}$x-2.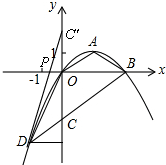
由$\left\{\begin{array}{l}y=\frac{{\sqrt{3}}}{3}x-2\\ y=-\frac{1}{3}{x^2}+\frac{{2\sqrt{3}}}{3}x\end{array}\right.$
得交点D的坐标为(-$\sqrt{3}$,-3),
令x=0得,y=-2,
∴C点的坐标为(0,-2),
由勾股定理,得:OA=2=OC,AB=2=CD,OB=2$\sqrt{3}$=OD.
在△OAB与△OCD中,
$\left\{\begin{array}{l}OA=OC\\ AB=CD\\ OB=OD\end{array}\right.$,
∴△OAB≌△OCD.
(3)点C关于x轴的对称点C'的坐标为(0,2),
∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,
∴PO∥DQ.
∴△C'PO∽△C'DQ.
∴$\frac{PO}{DQ}=\frac{C'O}{C'Q}$,
∴$\frac{PO}{{\sqrt{3}}}=\frac{2}{5}$,
∴PO=$\frac{2\sqrt{3}}{5}$,
∴点P的坐标为(-$\frac{2\sqrt{3}}{5}$,0).
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,全等三角形的性质和判定,相似三角形的性质和全等,解本题的关键是确定函数解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
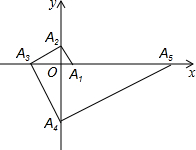 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
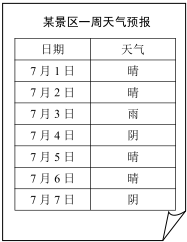 某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 角平分线上的点到角的两边的距离相等 | |
| B. | 直角三角形斜边上的中线等于斜边的一半 | |
| C. | 菱形的对角线相等 | |
| D. | 平行四边形是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过有交通信号灯的路口,遇到红灯 | |
| B. | 某妇产医院里,下一个出生的婴儿是女孩 | |
| C. | 367人中至少有2人生日(公历)相同 | |
| D. | 长分别为3、5、9厘米的三条线段能围成一个三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com