
【题目】如图,在△ABC和△DBE中,BC=BE,还需要添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
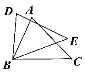
A. AC=DE,∠C=∠E B. BD=AB,AC=DE C. AB=DB,∠A=∠D D. ∠C=∠E,∠A=∠D
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】(1)设![]() 若
若![]() 求A-2B的值;
求A-2B的值;
(2)某公司有甲、乙两类经营收入,去年甲类收入是乙类收入的2倍,预计今年甲类年收入减少9%,乙类收入将增加19%。问今年该公司的年总收入比去年增加了吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究函数y=x+ ![]() 的图象与性质】
的图象与性质】
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中函数y=x+ ![]() 的图象大致是;
的图象大致是; 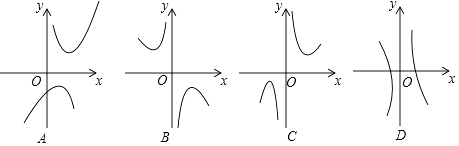
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
解:∵x>0
∴y=x+ ![]() =(
=( ![]() )2+(
)2+( ![]() )2=(
)2=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0
)2≥0
∴y≥ .
(4)若函数y= ![]() ,则y的取值范围 .
,则y的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD 是∠AOB 的平分线,∠AOC=2∠BOC.
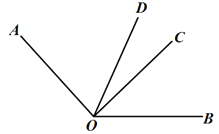
(1)若 AO⊥CO,求∠BOD 的度数;
(2)若∠COD=21°,求∠AOB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两个统计图. 
(1)本次调查的学生共有人,估计该校1200名学生中“不了解”的人数是人;
(2)“非常了解”的4人有A1 , A2两名男生,B1 , B2两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离. 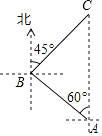
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
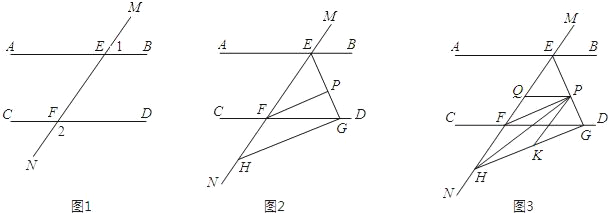
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD交于点O,OM⊥AB,
(1)若∠1=∠2,试判断ON与CD的位置关系,并说明理由.
(2)若∠1=![]() ∠BOC,试求∠MOD的度数.
∠BOC,试求∠MOD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com