
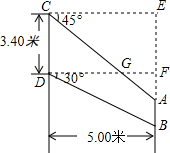
 某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ).
某型号飞机的机翼形状如图,根据图示尺寸计算AC和AB的长度(精确到0.1米,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73 ). 分析 在Rt△CAE中,∠ACE=45°,则△ACE是等腰直角三角形即可求得AC的长;在Rt△BFD中已知∠BDF与FB的长,进而得出AB的长.
解答  解:在Rt△CAE中,∠ACE=45°,
解:在Rt△CAE中,∠ACE=45°,
∴AE=CE=5(m),
∴AC=$\sqrt{2}$CE=5$\sqrt{2}$≈5×1.414≈7.1(m),
在Rt△BFD中,∠BDF=30°,
∴BF=FD•tan30°
=5×$\frac{\sqrt{3}}{3}$
≈5×$\frac{1.732}{3}$≈2.89(m),
∵DC=EF=3.4(m),
∴AF=1.6m,则AB=2.89-1.6=1.29≈1.3(m),
答:AC约为7.1米,BA约为1.3米.
点评 此题考查了三角函数的基本概念,主要是正切函数的概念及运算,关键把实际问题转化为数学问题加以计算.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:填空题
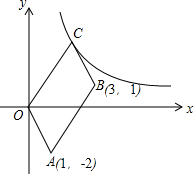 如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1),反比例函数y=$\frac{k}{x}$的图象过C点,则k的值为6.
如图,在平面直角坐标系中,四边形OABC是平行四边形,O(0,0),A(1,-2),B(3,1),反比例函数y=$\frac{k}{x}$的图象过C点,则k的值为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com