
【题目】为实现区域教育均衡发展,我市计划对某县![]() 、
、![]() 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所![]() 类学校和两所
类学校和两所![]() 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所![]() 类学校和一所
类学校和一所![]() 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所![]() 类学校和一所
类学校和一所![]() 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县![]() 、
、![]() 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到![]() 、
、![]() 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
【答案】(1)![]() (2)若该县的
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有15所.
类学校至少有15所.
(3)共有4种方案.
【解析】
(1)可根据“改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元”,列出方程组求出答案;
(2)根据“共需资金1575万元”“A类学校不超过5所”,进行判断即可;
(3)要根据“若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元”来列出不等式组,判断出不同的改造方案;
解:(1)设改造一所A类学校和一所B类学校所需的改造资金分别为a万元和b万元.
依题意得:![]() ,
,
解得:![]() ,
,
答:改造一所A类学校和一所B类学校所需的改造资金分别为60万元和85万元;
(2)设该县有A、B两类学校分别为m所和n所.
则60m+85n=1575,
m=![]() ,
,
∵A类学校不超过5所,
∴![]() ,
,
∴15≤n<18,
∵n为整数,
∴n=15,16,17.
当n=15,m=5符合题意,
即:B类学校至少有15所;
(3)设今年改造A类学校x所,则改造B类学校为(6-x)所,
依题意得:![]() ,
,
解得:1≤x≤4,
∵x取整数
∴x=1,2,3,4
答:共有4种方案.


科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.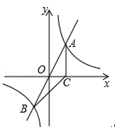
(1)求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E,DF 平分∠ADC 交边 BC 于 F,若 AD=11,EF=5,则 AB= ___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
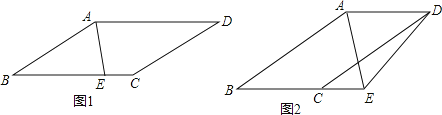
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证∠ABC=∠ADC;
②求∠CED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?
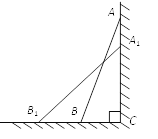
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com