
 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)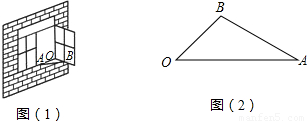
 解:(1)A.
解:(1)A.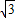 x.
x.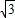 x=60,
x=60, =
= =30
=30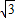 -30≈22(cm).
-30≈22(cm).

科目:初中数学 来源: 题型:
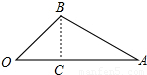
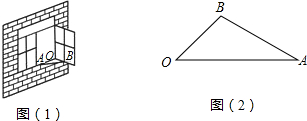 °,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
°,∠OAB=30°,OA=60cm,求点B到OA边的距离.(| 3 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年浙江省宁波东恩中学八年级上学期期中数学试卷(带解析) 题型:解答题
如图1,一扇窗户打开后用窗钩AB可将其固定.
(1)这里所运用的几何原理是( )
| A.三角形的稳定性 | B.两点之间线段最短 |
| C.两点确定一条直线 | D.垂线段最短 |
 ,结果精确到整数)
,结果精确到整数)
查看答案和解析>>
科目:初中数学 来源:第31章《锐角三角函数》中考题集(30):31.3 锐角三角函数的应用(解析版) 题型:解答题
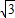 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)
查看答案和解析>>
科目:初中数学 来源:2010年中考数学十校联考模拟试卷(解析版) 题型:解答题
 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com