
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2 ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点B,则k的值为 .
的图象经过点B,则k的值为 . 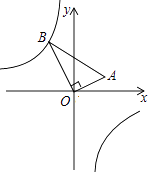
【答案】-8
【解析】解:过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,则∠OCA=∠BDO=90°,
∴∠DBO+∠BOD=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠DBO=∠AOC,
∴△DBO∽△COA,
∴ ![]() ,
,
∵点A的坐标为(2,1),
∴AC=1,OC=2,
∴AO= ![]() =
= ![]() ,
,
∴ ![]() ,即BD=4,DO=2,
,即BD=4,DO=2,
∴B(﹣2,4),
∵反比例函数y= ![]() 的图象经过点B,
的图象经过点B,
∴k的值为﹣2×4=﹣8.
故答案为:﹣8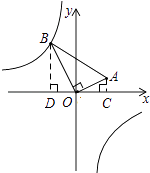
根据∠AOB=90°,先过点A作AC⊥x轴,过点B作BD⊥x轴,构造相似三角形,再利用相似三角形的对应边成比例,列出比例式进行计算,求得点B的坐标,进而得出k的值.本题主要考查了反比例函数图象上点的坐标特征以及相似三角形,注意:反比例函数图象上的点(x,y)的横、纵坐标的积是定值k,即xy=k,这是解决问题的关键.


科目:初中数学 来源: 题型:
【题目】甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为(![]() ,
,![]() ),请解决以下问题:
),请解决以下问题:
(1)甲比乙晚出发几小时?
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过![]() h与乙相遇.
h与乙相遇.
①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则ABCD的面积为( ) 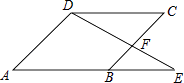
A.30
B.27
C.14
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为( )
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒时其中一个四边形为平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
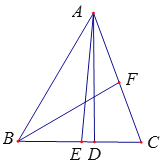
A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com