
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a≠0)的对称轴为直线x=﹣1.
(1)b= ;(用含a的代数式表示)
(2)当a=﹣1时,若关于x的方程ax2+bx+c=0在﹣4<x<1的范围内有解,求c的取值范围;
(3)若抛物线过点(﹣1,﹣1),当0≤x≤1时,抛物线上的点到x轴距离的最大值为4,求a的值.
【答案】(1)2a;(2)﹣1≤c<8;(3)a=![]() 或﹣
或﹣![]() .
.
【解析】
(1)利用对称轴公式,即可求解;
(2)该方程在在﹣4<x<1的范围内有解,则△=4+4c≥0,即可求解;
(3)抛物线上的点到x轴距离的最大值为4,即该点坐标为(1,4)或(1,﹣4),即可求解.
(1)x=![]() =﹣1,故b=2a,
=﹣1,故b=2a,
故答案为:2a;
(2)当a=﹣1时,函数表达式为:y=﹣x2﹣2x+c,
方程为:x2+2x﹣c=0,该方程在在﹣4<x<1的范围内有解,
则△=4+4c≥0,即c≥﹣1;
同时要满足:当x=﹣4时,y<0或x=1时,y<0,
即﹣16+8+c<0或﹣1﹣2+c<0,
故c<8或c<3,故c<8,
故﹣1≤c<8;
(3)抛物线过点(﹣1,﹣1),该点是抛物线的顶点,则函数的表达式为:y=a(x+1)2﹣1,
当0≤x≤1时,抛物线上的点到x轴距离的最大值为4,而顶点到x轴的距离为1,
则x=1时,该点的y坐标为4或﹣4,即该点坐标为(1,4)或(1,﹣4),
将点(1,4)或(1,﹣4),代入函数表达式得:
4=a(1+1)2﹣1或﹣4=a(1+1)2﹣1,
解得:a=![]() 或﹣
或﹣![]() .
.


科目:初中数学 来源: 题型:
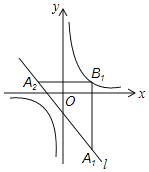
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=![]() ,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
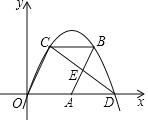
【题目】如图,点A为x轴上一点,点B的坐标为(a,b),以OA,AB为边构造OABC,过点O,C,B的抛物线与x轴交于点D,连结CD,交边AB于点E,若AE=BE,则点C的横坐标为( )
A.a﹣bB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
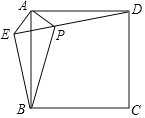
【题目】如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=2,PB=2![]() .则正方形ABCD的面积是_____.
.则正方形ABCD的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.

(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
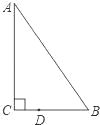
【题目】如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
A.70° B.70°或120°
C.120° D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() ,连接
,连接![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
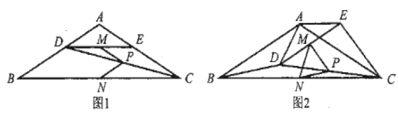
(1)观察猜想
图1中,线段![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 的度数是________;
的度数是________;
(2)探究证明
把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,连接
逆时针方向旋转到图2的位置,连接![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,请直接写出
,请直接写出![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com