
 完成下面推理过程.
完成下面推理过程.分析 由AB与CD平行,利用两直线平行,内错角相等得到一对角相等,再由EG与FH为角平分线,利用角平分线定义及等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(两直线平行,内错角相等).
∵EG平分∠AEF,FH平分∠EFD(已知).
∴∠GEF=$\frac{1}{2}$∠AEF,∠HFE=$\frac{1}{2}$∠EFD,(角平分线定义)
∴∠GEF=∠HFE,
∴EG∥FH(内错角相等,两直线平行).
故答案为:两直线平行,内错角相等;已知;GEF;HFE;角平分线的定义;GEF;HFE;内错角相等,两直线平行.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -3 | C. | -4 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
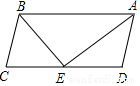 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤
如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 成轴对称的两个图形是全等图形 | |
| B. | 直角三角形斜边上的中线等于斜边的一半 | |
| C. | 若x>y,则x-3>y-3 | |
| D. | ∠A的相邻外角是70°,要使△ABC为等腰三角形,则∠B为35°或110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
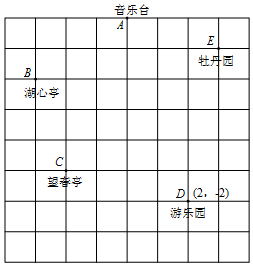 小王到公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示,可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),且一格表示一个单位长度.
小王到公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示,可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),且一格表示一个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com