Question

19．如图，正方形ABCD中，M为AD边上的一点，连接BM，过C点作CN∥BM，交AD的延长线于点N，在CN上截取CE=BC，连接BE交CD于F．
（1）若∠AMB=60°，CE=2$\sqrt{3}$，求DF的长；
（2）求证：BM=DN+CF；
（3）若F为CD的中点，求$\frac{AM}{AD}$的值．

Answer 1

分析 （1）利用正方形的性质以及已知得出∠MBE=∠CBE=$\frac{1}{2}$∠MBC=30°，进而得出CF的长，即可得出DF的长；
（2）首先证明△CBN≌△BAM，进而得出∠MBH=∠ABF，再得出BM=HM=AH+AM，即可得出答案．
（3）设AD=AB=x，AM=y，则AH=$\frac{1}{2}$x，BM=HM=$\frac{1}{2}$x+y，然后根据勾股定理得出x²+y²=（$\frac{1}{2}$x+y）²，整理即可求得$\frac{AM}{AD}$的值．

解答 （1）解：∵四边形ABCD是正方形，
∴∠DAB=∠ABC=∠BCD=∠CDA=90°，AD∥BC，
∵∠AMB=60°，
∴∠MBC=∠AMB=60°，
∵CE=BC，CE=2$\sqrt{3}$，
∴∠EBC=∠CEB，BC=CE=2$\sqrt{3}$，
∵CN∥BM，
∴∠MBE=∠CEB，
∴∠MBE=∠CBE=$\frac{1}{2}$∠MBC=30°，
又∵在Rt△BCF中，∠CBF=30°，
∴CF=$\frac{\sqrt{3}}{3}$BC=2，
又∵ABCD是正方形，
∴DC=BC=2$\sqrt{3}$，
∴DF=2$\sqrt{3}$-2；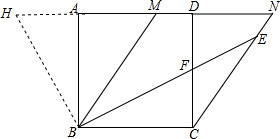

（2）证明：将△BCF绕着点B顺时针旋转90°得到△ABH，
∵ABCD是正方形，
∴AB=CD，∠BCD=∠A=90°，
∴∠CDN=∠A，
∵BM∥CN，
∴∠N=∠AMB，
在△CDN和△BAM中
$\left\{\begin{array}{l}{∠N=∠AMB}\\{∠BAM=∠CDN}\\{AB=CD}\end{array}\right.$
∴△CDN≌△BAM（AAS），
∴DN=AM，
又由旋转可知：CF=AH，∠CFB=∠H，∠BCF=∠BAH=90°，
∵∠BAD=90°，
∴∠BAD+∠BAH=180°，
∴点M、A、H在同一直线．
∴CF+DN=AH+AM=HM，
∵CE=BC，
∴∠EBC=∠CEB，
∵CN∥BM，
∴∠MBE=∠CEB，
∴∠MBE=∠CBE
又∵∠CBF=∠ABH，
∴∠GBE=∠CBM，
∴∠GBE+∠CBE=∠CBM+∠CBE，
即∠MBH=∠ABF，
又∵正方形ABCD中，AB∥CD，
∴∠BFC=∠EBA，
∴∠ABF=∠H，
∴∠H=∠MBH，
∴BM=HM=AH+AM，
∴BM=DN+CF．
（3）由（2）可知MH=BM，
∵F为CD的中点，
∴CF=$\frac{1}{2}$CD，
∴AH=$\frac{1}{2}$AB，
设AD=AB=x，AM=y，
∴AH=$\frac{1}{2}$x，
∴BM=HM=$\frac{1}{2}$x+y，
在Rt△ABM中，AM²+AB²=BM²，
∴x²+y²=（$\frac{1}{2}$x+y）²，
∴3x=4y，
∴$\frac{y}{x}$=$\frac{3}{4}$，
∴$\frac{AM}{AD}$=$\frac{3}{4}$．

点评 此题主要考查了全等三角形的判定与性质以及正方形的性质以及等角对等边等知识，根据旋转的性质得出BM=AH+AM=DN+CF是解题关键．