


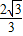 秒,点P从点A→O→B需要
秒,点P从点A→O→B需要 秒,所以分两种情况讨论:①0<t<
秒,所以分两种情况讨论:①0<t< ;②
;② ≤t<
≤t<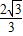 .针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围;
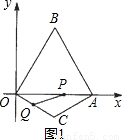
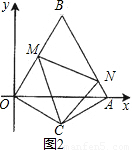
.针对每一种情况,根据P点所在的位置,由三角形的面积公式得出△OPQ的面积S与运动的时间t之间的函数关系,并且得出自变量t的取值范围;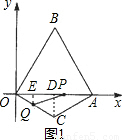 解:(1)过点C作CD⊥OA于点D.(如图)
解:(1)过点C作CD⊥OA于点D.(如图)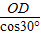 =
=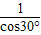 =
=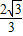 (1分)
(1分) 时,OQ=t,AP=3t,OP=OA-AP=2-3t.
时,OQ=t,AP=3t,OP=OA-AP=2-3t.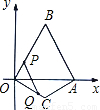
 OQ=
OQ= ,
, OP•EQ=
OP•EQ= (2-3t)•
(2-3t)• =-
=-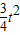 +
+ t,
t,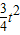 +
+ t;(3分)
t;(3分) <t≤
<t≤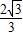 时(如图)
时(如图) OQ•OP=
OQ•OP= t•(3t-2)=
t•(3t-2)=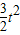 -t,
-t,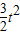 -t;
-t; 时,S=-
时,S=-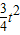 +
+ t,当
t,当 <t≤
<t≤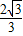 时,S=
时,S=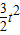 -t(5分)
-t(5分)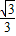 ,1)或(
,1)或(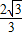 ,0)或(
,0)或( ,0)或(
,0)或( ,
,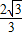 )(9分)
)(9分)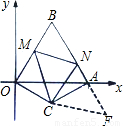
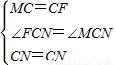 ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2010年全国中考数学试题汇编《锐角三角函数》(06)(解析版) 题型:解答题
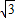 .点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).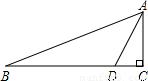
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《四边形》(11)(解析版) 题型:解答题
 ∠FCM.
∠FCM.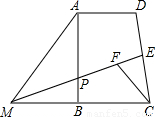
查看答案和解析>>
科目:初中数学 来源:2010年重庆市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年重庆市中考数学试卷(解析版) 题型:解答题
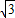 .点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).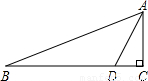
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com