
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.
求证:AC∥DF.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,在△ABC中,已知∠ABC=35°,点D在BC上,点E在AC上,∠BAD=∠EBC,AD交BE于F.
(1)求∠BFD的度数;
(2)若EG//AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
若∠C= ,∠EAC+∠FBC=
,∠EAC+∠FBC=
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则 与
与 有何关系?并说明理由.
有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)
(3)如图③,若 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于 ,
,  ;依此类推,则
;依此类推,则 = (用
= (用 、
、 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知直线 ,直线
,直线 与
与 、
、 分别交于
分别交于 、
、 两点,点
两点,点 是直线
是直线 上的一动点
上的一动点
如图,若动点 在线段
在线段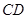 之间运动(不与
之间运动(不与 、
、 两点重合),问在点
两点重合),问在点 的运动过程中是否始终具有
的运动过程中是否始终具有 这一相等关系?试说明理由;
这一相等关系?试说明理由;
如图,当动点 在线段
在线段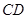 之外且在的上方运动(不与
之外且在的上方运动(不与 、
、 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在四边形ABCD中,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=208°,求∠OBC+∠OCB的度数。请你将解答过程补充完整。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com