
 如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.
如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y 平方米,AB长为x米.分析 (1)根据AB为xm,BC就为(24-3x)m,利用长方形的面积公式,可求出关系式;
(2)根据墙的最大可用长度a=15米列不等式求出自变量x的取值范围;
(3)由(1)可知y和x为二次函数关系,根据二次函数的性质即可求围成的长方形花圃的最大面积及对应的AB的长;
解答 解:(1)y=x(24-3x)=-3x2+24x;
(2)∵0<24-3x≤15,
∴3≤x<8;
(3)y=-3x2+24x=-3(x-4)2+48,
∵3≤x<8;
∴当x=4时,y最大=48,即当AB=4米时,最大面积为48平方米.
点评 本题主要考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数表达式,再根据二次函数性质解决问题.特别要注意垂直于墙的有三道篱笆.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
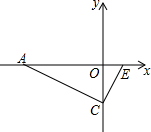 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C(0,-2).如果BC=$\sqrt{5}$,∠ACB=90°.求这个二次函数解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com