
分析 将x=-1代入原方程,看原方程是否成立,由此即可得出-1是否为方程的根,再方程的两个根为m、n,由两根之积为mn=$\frac{c-a}{a-b}$结合m=-1即可求出n的值.
解答 解:当x=-1时,∵(a-b)+(b-c)+c-a=0,
∴-1是方程(a-b)x2-(b-c)x+c-a=0(a≠b)的一个根.
设方程的两个根为m、n且m=-1,
∵mn=$\frac{c-a}{a-b}$,m=-1,
∴n=$\frac{a-c}{a-b}$.
故-1是方程(a-b)x2-(b-c)x+c-a=0(a≠b)的一个根,方程的另一个根为$\frac{a-c}{a-b}$.
点评 本题考查了根与系数的关系,解题的关键是找出mn=$\frac{c-a}{a-b}$.本题属于基础题,难度不大,解决该题型题目时,根据方程的系数找出两根之和与两根之积是关键.


科目:初中数学 来源: 题型:解答题
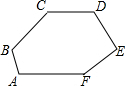 如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)
如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形BCDE中,DE∥BC,CD、BE的延长线交于点A,联结BD、CE相交于点O,已知AE=3,EB=6,DE=2.
如图,梯形BCDE中,DE∥BC,CD、BE的延长线交于点A,联结BD、CE相交于点O,已知AE=3,EB=6,DE=2.查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省佛山市顺德区七年级3月月考数学试卷(解析版) 题型:填空题
如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由______________.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
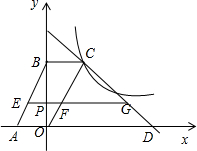 如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com