
【题目】如图,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,请按照图中所标注的数据计算图中实线所围成的图形的面积
,请按照图中所标注的数据计算图中实线所围成的图形的面积![]() ______.
______.

【答案】50
【解析】
根据∠F=∠AGB=∠EAB=90°,证明∠FEA=∠BAG,再根据AAS证△FEA≌△GAB,推出AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,求出FH=14,根据阴影部分的面积=S梯形EFHD-S△EFA-S△ABC-S△DHC和面积公式代入求出即可.
∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中,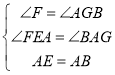 ,
,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理可证:△CBG≌△DCH(AAS),
∴CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面积=![]() ×(EF+DH)×FH=
×(EF+DH)×FH=![]() ×(6+4)×14=70,
×(6+4)×14=70,
∴阴影部分的面积=S梯形EFHDS△EFAS△ABCS△DHC
=70![]() ×6×2
×6×2![]() ×(6+4)×2
×(6+4)×2![]() ×4×2
×4×2
=50.
故答案为50.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点G.
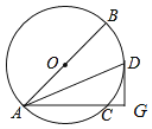
求证:(1)DG⊥AG;
(2)AG+CG=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
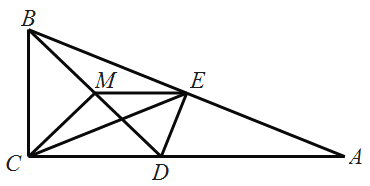
(1)求证: CM= EM;
(2)当线段AC长度改变时, △CME与△ABD的面积之比是否发生变化?如果不变,求出比值;如果发生变化。说明如何变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:

如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是: ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究题
在之前的学习中,我们已经初步了解到,长方形的对边平行且相等,每个角都是![]() .如图,长方形
.如图,长方形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 上一动点,从点
上一动点,从点![]() 出发,以
出发,以![]() 向终点
向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以
出发,以![]() 向终点
向终点![]() 运动,运动的时间为
运动,运动的时间为![]() .
.
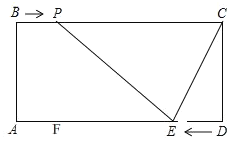
(1)当![]() 时,①则线段
时,①则线段![]() 的长=______;
的长=______;
②当![]() 平分
平分![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值;
的值;
(3)连接![]() ,直接写出点
,直接写出点![]() 与点
与点![]() 关于
关于![]() 对称时
对称时![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作![]() 小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com