
 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )| A. | 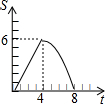 | B. | 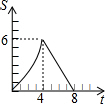 | C. |  | D. | 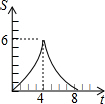 |
分析 可以分为两种情况:当M、N分别在OA、OC上时,可证明△OMN∽△OAC,由题意可求得OM、ON的长,即可求得面积的表达式;当M、N分别在AB、BC上时,由△DAM∽△AOC,可得AM,由△BMN∽△BAC,可得BN,即可得BM、CN,由S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积,可得关于t的表达式,然后根据函数的图象的形状确定正确的选项即可.
解答 解:∵四边形OABC是矩形,点B的坐标为(4,3),
∴A(4,0),C(0,3),
当0<t≤4时,OM=t,
由△OMN∽△OAC,
得$\frac{OM}{OA}$=$\frac{ON}{OC}$,
∴ON=$\frac{3}{4}$t,S=$\frac{3}{8}$t2;
当4<t<8时,
如图,∵OD=t,
∴AD=t-4.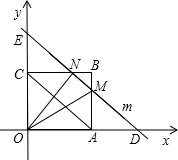
由△DAM∽△AOC,可得AM=$\frac{3}{4}$(t-4)
∴BM=6-$\frac{3}{4}$t.
由△BMN∽△BAC,可得BN=$\frac{4}{3}$BM=8-t
∴CN=t-4
S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积
=12-$\frac{3}{2}$(t-4)-$\frac{1}{2}$(8-t)(6-$\frac{3}{4}$t)-$\frac{3}{2}$(t-4)=-$\frac{3}{8}$t2+3t,
故选C.
点评 考查了动点问题的函数图象,重点应用了相似三角形的判定和性质以及分类讨论的数学思想,难度较大.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
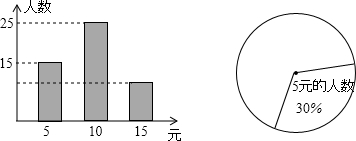
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
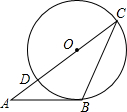 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )
如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.如果∠A=34°,那么∠C等于( )| A. | 28° | B. | 33° | C. | 34° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.01×10-6kg | B. | 2.01×10-5kg | C. | 20.1×10-7kg | D. | 20.1×10-6kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com