
【题目】如图1,![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标
点坐标![]() 为且
为且![]() .
.
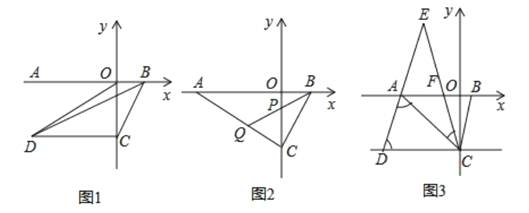
(1)求![]() 两点的坐标;
两点的坐标;
(2)求![]() ;
;
(3)如图2,若![]() 点坐标为
点坐标为![]() 点坐标为
点坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,
上一点,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,若
,若![]() ,求出点
,求出点![]() 坐标.
坐标.
(4)如图3,若![]() ,点
,点![]() 在
在![]() 轴正半轴上任意运动,
轴正半轴上任意运动,![]() 的平分线
的平分线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 点的运动过程中,
点的运动过程中,![]() 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由.
【答案】(1)C(0,-2),D(-3,-2);(2)3;(3)Q(![]() ,
,![]() );(4)
);(4)![]() 值不变,且为
值不变,且为![]()
【解析】
(1)根据![]() 中绝对值和算术平方根的非负性可求得a和b的值,从而得到C和D的坐标;
中绝对值和算术平方根的非负性可求得a和b的值,从而得到C和D的坐标;
(2)求出CD的长度,再根据三角形的面积公式列式计算即可;
(3)根据![]() 可得△ABQ的面积等于△BOC的面积,求出△OBC的面积,再根据AB的长度可求得点Q的纵坐标,然后求出直线AC的表达式,代入点Q纵坐标即可求出点Q的横坐标;
可得△ABQ的面积等于△BOC的面积,求出△OBC的面积,再根据AB的长度可求得点Q的纵坐标,然后求出直线AC的表达式,代入点Q纵坐标即可求出点Q的横坐标;
(4)在△AOE和△BFC中,利用三角形内角和定理列式整理表示出∠ABC,然后相比即可得解.
解:(1)∵![]() ,
,
∴a+2=0,b+3=0,
∴a=-2,b=-3,
∴C(0,-2),D(-3,-2);
(2)∵C(0,-2),D(-3,-2),
∴CD=3,且CD∥x轴,
∴![]() =
=![]() ×3×2=3;
×3×2=3;
(3)∵![]() ,△OBP为公共部分,
,△OBP为公共部分,
∴S△ABQ=S△BOC,
∵B(2,0),C(0,-2)
∴S△BOC=![]() =2= S△ABQ,
=2= S△ABQ,
∵A(-3,0),
∴AB=5,
S△ABQ=![]() =2,
=2,
∴![]() ,
,
设直线AC的表达式为y=kx+b,
将A,C坐标代入,
![]() ,
,
解得: ,
,
∴直线AC的表达式为:![]() ,
,
令y=![]() ,
,
解得x=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() );
);
(4)在△ACE中,设∠ADC=∠DAC=α,∠ACE=β,
∠E=∠DAC-∠ACE=α-β,
∵CE平分∠ACB,
∴∠BCE=∠ACE=β,
在△AFE和△BFC中,
∠E+∠EAF+∠AFE=180°,
∠ABC+∠BCF+∠BFC=180°,
∵CD∥x轴,
∴∠EAF=∠ADC=α,
又∵∠AFE=∠BFC,
∴∠E+∠EAF=∠ABC+∠BCF,
即α-β+α=∠ABC+β,
∴∠ABC=2(α-β),
∴![]() =
=![]() =
=![]() ,为定值.
,为定值.


科目:初中数学 来源: 题型:
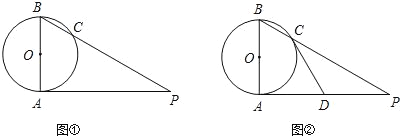
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
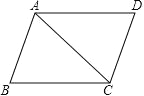
【题目】如图,四边形ABCD 是平行四边形,AB=c,AC=b,BC=a,抛物线 y=ax2+bx﹣c 与 x 轴的一个交点为(m,0).
(1)若四边形ABCD是正方形,求抛物线y=ax2+bx﹣c的对称轴;
(2)若 m=![]() c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
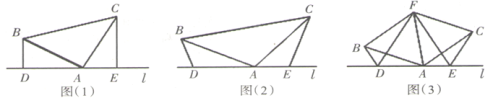
【题目】(1)问题发现:如图(1),已知:在三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() ,试写出线段
,试写出线段![]() 和
和![]() 之间的数量关系为_________________.
之间的数量关系为_________________.
(2)思考探究:如图(2),将图(1)中的条件改为:在![]() 中,
中, ![]() 三点都在直线
三点都在直线![]() 上,并且
上,并且![]() ,其中
,其中![]() 为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展应用:如图(3),![]() 是
是![]() 三点所在直线
三点所在直线![]() 上的两动点,(
上的两动点,(![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 与
与![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,若
,若![]() ,试判断
,试判断![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
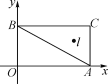
【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACE是以平行四边行ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(10,-4![]() ),则D点的坐标是( )
),则D点的坐标是( )

A.(6,0)B.(6![]() ,0)C.(8,0)D.(8
,0)C.(8,0)D.(8![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
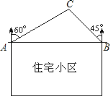
【题目】某住宅小区如图所示,小区东西两端的楼![]() 、
、![]() 之间的距离为
之间的距离为![]() ,某开发商准备在位于
,某开发商准备在位于![]() 楼的北偏东
楼的北偏东![]() 方向,且在
方向,且在![]() 楼的北偏西
楼的北偏西![]() 方向上的
方向上的![]() 处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆
处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆![]() 处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据
处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com