
【题目】已知射线![]() 平行于射线
平行于射线![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上.
上.

(1)如图1,若点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() 时,则
时,则![]() _________.
_________.
(2)如图1,若点![]() 在线段
在线段![]() 上运动(不包含
上运动(不包含![]() 、
、![]() 两点),则
两点),则![]() 、
、![]() 、
、![]() 之间的等量关系是_____________________.
之间的等量关系是_____________________.
(3)①如图2,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________;
之间的等量关系是________________;
②如图3,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________.
之间的等量关系是________________.
(4)请说明图2中所得结论的理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() ;(4)见解析;
;(4)见解析;
【解析】
(1)过P作GH∥CD,根据平行线的性质得∠HPC=∠C,由AB∥CD得到AB∥GH,得到∠APH=∠A,则∠APC=∠HPC+∠APH=∠A+∠C,把∠A=25°,∠APC=70°代入计算可得到∠C的度数;
(2)过P作GH∥CD,根据平行线的性质得∠HPC=∠C,由AB∥CD得到AB∥GH,得到∠APH=∠A,则∠APC=∠HPC+∠APH=∠A+∠C,可得到∠APC=∠A+∠C;
(3)过P作MN∥CD,根据平行线的性质得∠MPC=∠C,由AB∥CD得到AB∥MN,得到∠APM=∠A,则∠APC=∠MPC-∠APM=∠C-∠A,可得到∠APC=∠C-∠A;
② 过P作IJ∥CD,根据平行线的性质得∠IPC=∠C,由AB∥CD得到AB∥IJ,得到∠API=∠A,则∠APC=∠API-∠IPC=∠A-∠C,可得到∠APC=∠A-∠C;
(4)过点![]() 作
作![]() ,由两直线平行,内错角相等,得到
,由两直线平行,内错角相等,得到![]() ,
,![]() ,再由角的关系进行相减即可.
,再由角的关系进行相减即可.
解:
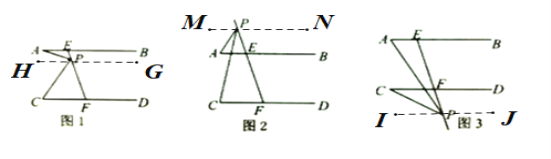
(1)如图1,过P作GH∥CD,
∴∠C=∠CPH.
∵AB∥CD,
∴AB∥GH,
∴∠A=∠APH.
∵∠APC=∠HPC+∠APH=∠A+∠C,
∴∠C=∠APC-∠A=70°-25°=45°.
(2)如图1,如图1,过P作GH∥CD,
∴∠C=∠CPH.
∵AB∥CD,
∴AB∥GH,
∴∠A=∠APH.
∵∠APC=∠HPC+∠APH=∠A+∠C,
∴![]() .
.
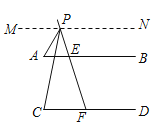
(3)①如图2,过P作MN∥CD,
∴∠MPC=∠C.
∵AB∥CD,
∴AB∥MN,
∴∠APM=∠A.
∵∠APC=∠MPC-∠APM=∠C-∠A
∴![]() ;
;
②如图3,过P作IJ∥CD,
∴∠IPC=∠C.
∵AB∥CD,
∴AB∥IJ,
∴∠API=∠A.
∵∠APC=∠API-∠IPC=∠A-∠C
∴![]() .
.
(4)理由:过点![]() 作
作![]()
∵![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学着说点理:补全证明过程:
如图,AB∥EF,CD⊥EF于点D,若∠B=40°,求∠BCD的度数.

解:过点C作CG∥AB.
∵AB∥EF,
∴CG∥EF.( )
∴∠GCD=∠ .(两直线平行,内错角相等)
∵CD⊥EF,
∴∠CDE=90°.( )
∴∠GCD= .(等量代换)
∵CG∥AB,
∴∠B=∠BCG.( )
∵∠B=40°,
∴∠BCG=40°.
则∠BCD=∠BCG+∠GCD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
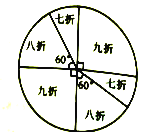
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 CD 是经过∠BCA 顶点 C 的一条直线,CA=CB.E、F 分别是直线 CD 上两点(不 重合),且∠BEC=∠CFA=∠a
(1)若直线 CD 经过∠BCA 的内部,且 E、F 在射线 CD 上,请解决下面问题:
①若∠BCA=90°,∠a=90°,请在图 1 中补全图形,并证明:BE=CF,EF=![]() ;
;
②如图 2,若 0°<∠BCA<180°,请添加一个关于∠a 与∠BCA 关系的条件 , 使①中的两个结论仍然成立;
(2)如图 3,若直线 CD 经过∠BCA 的外部,∠a=∠BCA,请写出 EF、BE、AF 三条线 段数量关系(不要求证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com