
【题目】如图,已知抛物线![]() 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
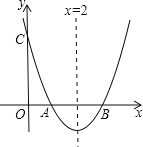
(1)求抛物线的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
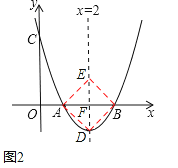
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为 .
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)(2,﹣1)
;(3)(2,﹣1)
【解析】
(1)根据抛物线对称轴的定义易求A(1,0),B(3,0),所以设抛物线的顶点式![]() ,将点A的坐标代入即可求得h,得到抛物线的函数表达式.
,将点A的坐标代入即可求得h,得到抛物线的函数表达式.
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可.
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线![]() 的顶点坐标,即(2,﹣1).
的顶点坐标,即(2,﹣1).
解:(1)∵AB=2,对称轴为直线x=2,
∴点A的坐标是(1,0),点B的坐标是(3,0).
设抛物线的函数表达式为![]() ,
,
将A(1,0)代入得:![]() ,解得
,解得![]() .
.
∴抛物线的函数表达式为![]() ,即
,即![]() .
.
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.
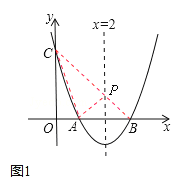
由(1)抛物线解析式为![]() ,A(1,0),B(3,0),
,A(1,0),B(3,0),
∴C(0,3).
∴![]() ,
,![]() .
.
∵点A、B关于对称轴x=2对称,∴PA=PB.∴PA+PC=PB+PC.此时,PB+PC=BC.
∴点P在对称轴上运动时,(PA+PB)的最小值等于BC.
∴△APC的周长的最小值=AC+AP+PC=AC+BC=![]() .
.
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线y=x2-4x+3的顶点坐标,即(2,-1),
当E、D点在x轴的上方,即DE∥AB,AE=AB=BD=DE=2,此时不合题意,
故点D的坐标为:(2,-1).


科目:初中数学 来源: 题型:
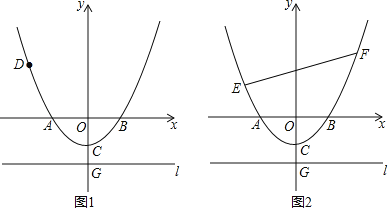
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=![]() x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
(1)求抛物线对应的二次函数的解析式;
(2)若D(﹣4,m)为抛物线y=![]() x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
(3)如图2,若E(﹣4,m)为上述抛物线上一点,在抛物线上是否存在点F,使得△BEF是直角三角形,若存在求出点F的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
B.“抛一枚硬币,正面朝上的概率为![]() ”,表示每抛掷两次就有一次正面朝上
”,表示每抛掷两次就有一次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是6的概率为![]() ”,表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的概率稳定在
”,表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的概率稳定在![]() 附近
附近
D.某种彩票的中奖概率为![]() ,买1000张这种彩票一定有一张中奖
,买1000张这种彩票一定有一张中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
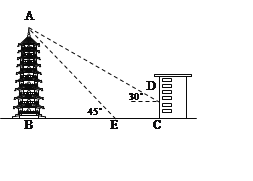
【题目】某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.

(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=![]() 的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.
的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com