
��ͼ����A������Ϊ ����B������Ϊ
����B������Ϊ ����C������Ϊ
����C������Ϊ .
.
������ƽ��ֱ������ϵ�л���?ABC����ƽ��2����λ���ͼ��?A1B1C1.
������ֱ������ϵ�л���?ABC�Ƶ�C��ʱ����ת90���������Ϊ?A��B��C�䣬ֱ��д����A�������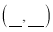 , ��B�������
, ��B������� .
.

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��֪��O�뾶Ϊ1��A��B�ڡ�O�ϣ��� ����AB���Ե�Բ�ܽ�Ϊ__o.
����AB���Ե�Բ�ܽ�Ϊ__o.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������������2017-2018ѧ���һѧ�ڰ��꼶��ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ֽ�ǹ��ϵĺ��������������ֽ�Ĺ��߲��ϼ���ռ��������������գ��������������������������ԣ��������һ������ʽ�ӹŵ������鼰�ҹ��ij�����壬�������Ⱥ�ڵ�ϲ������������۲������ķ���ֽͼ�������в�����Գ�ͼ�ε��ǣ�������
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȵ�һѧ�ں����а��꼶��ѧ����ĩ���ģ���⣨ʵ������ ���ͣ���ѡ��
�������߶�a��b��c�ij�Ϊ�ߣ��ܹ���ֱ�������ε��ǣ� ��
A. a=4, b=5, c=6 B. a=6, b=8, c=12
C. a=1, b=2, c= D. a=
D. a= ��b=2��c=
��b=2��c=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�Թ���2017��2018ѧ����ѧ�ھ��꼶��ĩͳһ������ѧ�Ծ� ���ͣ������
��ͼ����֪һ��ֱ�߹��� ������������
������������ ����
���� ���㣬���е�
���㣬���е� �ĺ�������
������� .
.
��������ֱ�ߵĺ�����ϵʽ����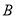 ������ ��
������ ��
���� �����Ƿ���ڵ�
�����Ƿ���ڵ� ,ʹ�á�
,ʹ�á� ��ֱ�������Σ������ڣ������
��ֱ�������Σ������ڣ������ �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
�ǹ��߶� ��һ��
��һ�� ,��
,�� ��
�� �ᣬ���������ڵ�
�ᣬ���������ڵ� ,��
,�� �ڵ�һ���ޣ���
�ڵ�һ���ޣ��� ������
������ �ĺ�����Ϊ��ֵʱ��
�ĺ�����Ϊ��ֵʱ�� 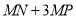 �ij���������ֵ�Ƕ��٣�
�ij���������ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�Թ���2017��2018ѧ����ѧ�ھ��꼶��ĩͳһ������ѧ�Ծ� ���ͣ������
�� ��һԪ���η��̣���
��һԪ���η��̣��� ��ֵΪ_________ .
��ֵΪ_________ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�Թ���2017��2018ѧ����ѧ�ھ��꼶��ĩͳһ������ѧ�Ծ� ���ͣ���ѡ��
������ ��ͼ����������
��ͼ����������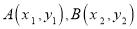 ����
����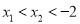 ���� ��
���� ��
A. 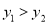 B.
B.  C.
C.  D.
D.  �Ĵ�С��ȷ��
�Ĵ�С��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݴ���2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ����֪ ��ƽ�ǣ�
��ƽ�ǣ�  ƽ��
ƽ�� ����ƽ���ϻ�����
����ƽ���ϻ����� ��ʹ
��ʹ ��
�� ���࣬��
���࣬�� ����
���� ��__________��
��__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018����꼶���ϣ���ѧ��ѧ�Ծ���9�·ݣ� ���ͣ������
�����κ���y=ax2+4x+a��1����Сֵ��2����a��ֵ��_____��
4 ������������������߶��κ���y=ax2��4x+a��1����Сֵ2�� ��a��0�� y��Сֵ=�� ��������a2��3a��4=0�� ���a=��1��4�� ��a��0�� ��a=4�� �ʴ�Ϊ��4�� ���ں��أ�����κ��������С��ֵ�����ַ�������һ�ֿ���ͼ��ֱ�ӵó����ڶ������䷽�����������ǹ�ʽ�������õ��Ǻ����ַ�����������ϵ��a�ľ���ֵ�ǽ�С������ʱ����...�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com