【答案】
分析:(1)根据直线y=kx+3与y轴相交于点C,得C(0,3),由tan∠OBC=1可求得点B(3,0);所以a=-1,即y=-x
2+2x+3=-(x-1)
2+4,顶点D(1,4),代入一次函数可知k=1.
(2)在y轴上取一点F(0,-3),则OF=OC=3,由对称性可知:∴∠CBF=90°,设直线BF与二次函数y=-x
2+2x+3的图象交于点P,由(1)知B(3,0),直线BF的函数关系式为y=x-3,联立方程组求解可得点P(-2,-5),所以存在点P(1,4)或P(-2,-5),使得△PBC是以BC为一条直角边的直角三角形.
解答:解:(1)由直线y=kx+3与y轴相交于点C,得C(0,3)
∵tan∠OBC=1
∴∠OBC=45°∴OB=OC=3
∴点B(3,0)(1分)
∵点B(3,0)在二次函数y=ax
2+2x+3的图象上
∴9a+6+3=0(2分)
∴a=-1(3分)
∴y=-x
2+2x+3=-(x-1)
2+4
∴顶点D(1,4)(4分)
又∵D(1,4)在直线y=kx+3上
∴4=k+3
∴k=1
即:a=-1,k=1.(5分)
(2)在二次函数y=-x
2+2x+3的图象上存在点P,使得△PBC是以BC为一条直角边的直角三角形(6分)
由(1)可知,直线y=x+3与x轴的交点为E(-3,0)
∴OE=OC=3
∴∠CEO=45°
∵∠OBC=45°
∴∠ECB=90°(7分)
∴∠DCB=90°
∴△DCB是以BC为一条直角边的直角三角形,且点D(1,4)在二次函数的图象上,则点D是所求的P点(8分)
方法一:设∠CBP=90°,点P在二次函数y=-x
2+2x+3的图象上,则△PBC是以BC为一条直角边的直角三角形,
∵∠CBO=45°
∴∠OBP=45°设直线BP与y轴交于点F,则F(0,-3)
∴直线BP的表达式为y=x-3(9分)
解方程组

得

或

由题意得,点P(-2,-5)为所求.
综合①②,得二次函数y-x
2+2x+3的图象上存在点P(1,4)或
P(-2,-5),使得△PBC是以BC为一条直角边的直角三角形(10分)
方法二:在y轴上取一点F(0,-3),则OF=OC=3,由对称性可知,
∠OBF=∠OBC=45°
∴∠CBF=90°设直线BF与二次函数y=-x
2+2x+3的图象交于点P,由(1)知B(3,0),
∴直线BF的函数关系式为y=x-3(以下与方法一同)(9分)
解方程组

得

或

由题意得,点P(-2,-5)为所求.
综合①②,得二次函数y-x
2+2x+3的图象上存在点P(1,4)或
P(-2,-5),使得△PBC是以BC为一条直角边的直角三角形.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.



 或
或

 或
或


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案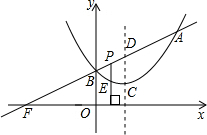 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.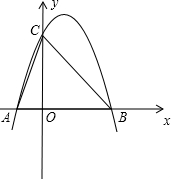
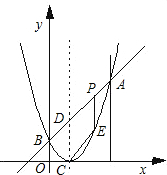 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.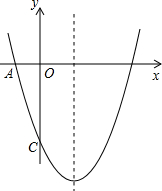 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).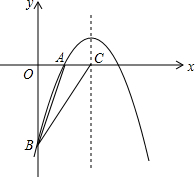 (2012•衡水一模)如图,已知二次函数y=-
(2012•衡水一模)如图,已知二次函数y=-