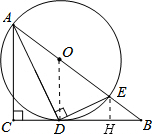
(1)证明:连接OD,
∵△ADE是直角三角形,OA=OE,
∴OD=OA=OE,
∴点D在⊙O上;
(2)证明:∵AD是∠BAC的角平分线,
∴∠CAD=∠DAB,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠C=∠ODB=90°,
∴BC是⊙O的切线;
(3)解:在Rt△ACB中,AC=6,BC=8,
∴根据勾股定理得:AB=10,
设OD=OA=OE=x,则OB=10-x,
∵AC∥OD,△ACB∽△ODB,
∴

=
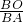
=

,即

=

,
解得:x=

,
∴OD=

,BE=10-2x=10-

=

,
∵

=

,即
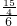
=
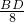
,
∴BD=5,
过E作EH⊥BD,
∵EH∥OD,
∴△BEH∽△BOD,
∴
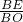
=
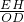
,即
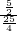
=
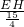
,
∴EH=

,
∴S
△BDE=

BD•EH=

.
分析:(1)连接OD,由DO为直角三角形斜边上的中线,得到OD=OA=OE,可得出点D在圆O上;
(2)由AD为角平分线,得到一对角相等,再由OD=OA,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OD与AC平行,根据两直线平行同位角相等即可得到∠ODB为直角,即BC与OD垂直,即可确定出BC为圆O的切线;
(3)过E作EH垂直于BC,由OD与AC平行,得到△ACB与△ODB相似,设OD=OA=OE=x,表示出OB,由相似得比例列出关于x的方程,求出方程的解得到x的值,确定出OD与BE的长,进而确定出BD的长,再由△BEH与△ODB相似,由相似得比例求出EH的长,△BED以BD为底,EH为高,求出面积即可.
点评:此题考查了切线的判定,相似三角形的判定与性质,勾股定理,平行线的判定与性质,熟练掌握切线的判定方法是解本题的关键.

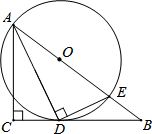 如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.
如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O. (1)证明:连接OD,
(1)证明:连接OD, =
=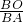 =
= ,即
,即 =
= ,
, ,
, ,BE=10-2x=10-
,BE=10-2x=10- =
= ,
, =
= ,即
,即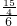 =
=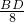 ,
,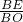 =
=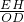 ,即
,即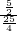 =
=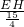 ,
, ,
, BD•EH=
BD•EH= .
.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为