
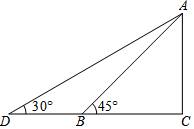
 如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上.
如图所示,某幼儿园为加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上.分析 (1)先在Rt△ABC中利用45°的正切计算出AC=2$\sqrt{2}$,再在Rt△ADC中利用含30度的直角三角形三边的关系得到AD≈5.656(m),然后计算AD-AB即可;
(2)利用等腰直角三角形的性质得到BC=AC=2$\sqrt{2}$,再在Rt△ADC中利用30度的正切计算出CD=2$\sqrt{6}$,则BD≈2.070,所以5-2.070=2.930<3,由于滑滑板的正前方有3米长的空地就能保证安全,则可判定这样改造不可行.
解答 解:(1)在Rt△ABC中,∵tan∠ABC=$\frac{AC}{AB}$,
∴AC=4tan45°=2$\sqrt{2}$,
在Rt△ADC中,∵∠D=30°,
∴AD=2AC=4$\sqrt{2}$≈5.656(m),
∵AD-AB=5.656-4≈1.66(m),
∴改善后滑滑板会加长1.66米;
(2)不可行,理由如下:
∵△ABC为等腰直角三角形,
∴BC=AC=2$\sqrt{2}$,
在Rt△ADC中,∵tanD=$\frac{AC}{CD}$,
∴CD=$\frac{2\sqrt{2}}{tan30°}$=$\frac{2\sqrt{2}}{\frac{\sqrt{3}}{3}}$=2$\sqrt{6}$,
∴BD=CD-BC=2$\sqrt{6}$-2$\sqrt{2}$≈2.07,
而5-2.07=2.930<3,
∴这样改造不可行.
点评 本题考查了解直角三角形的应用,要求同学们能利用三角函数求出表示出线段的长度.


科目:初中数学 来源: 题型:填空题
 如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$.
如图,已知P是边长为1的正三角形ABC内的一个动点,如PE⊥AB于E,PF⊥BC于F,PD⊥AC于D,则PD+PE+PF的值为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.
已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com