化简: .然后在不等式的非负整数解中选择一个适当的数代入求值．原式=.当x=0时.原式=2 [解析]洪量分析:首先利用分式的混合运算法则将原式化简.然后解不等式.选择使得分式有意义的值代入求解即可求得答案． [解答][解析] 原式= = = = ∵不等式x≤2的非负整数解是0.1.2 ∵≠0.x+2≠0. ∴x≠±1.x≠-2. ∴把x=0代入＝2．题目和参考答案——青夏教育精英家教网—

化简：，然后在不等式的非负整数解中选择一个适当的数代入求值．

原式=，当x=0时，原式=2 【解析】洪量分析：首先利用分式的混合运算法则将原式化简，然后解不等式，选择使得分式有意义的值代入求解即可求得答案．【解答】【解析】原式= = = = ∵不等式x≤2的非负整数解是0，1，2 ∵（x+1）（x-1）≠0，x+2≠0， ∴x≠±1，x≠-2， ∴把x=0代入＝2．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：解答题

如图,已知A(?4,2)、B(a,?4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点；

(1)求此反比例函数和一次函数的解析式；

(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；

(1)反比例函数的解析式为，一次函数的解析式为y=-x-2（2）-42 【解析】试题分析：（1）把A点坐标代入反比例函数解析式求出m的值，再把B点坐标代入反比例函数解析式求出a的值，从而得出点B的坐标，根据点A、B的坐标利用待定系数法即可求出直线AB的解析式；（2）由两函数图象的上下位置关系结合交点的横坐标，即可得出使一次函数值小于反比例函数值的x的取值范围．试...

查看答案和解析>>

科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：单选题

小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿，接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一小会儿，小华继续录入并加快了录入速度，直至录入完成，设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x之间的关系的大致图象是（）

A. B. C. D.

C 【解析】【解析】 A．暂停后继续录入并加快了录入速度，字数增加，故A不符合题意； B．字数先增加再不变最后增加，故B不符合题意错误； C．开始字数增加的慢，暂停后再录入字数增加的快，故C符合题意； D．中间应有一段字数不变，不符合题意，故D错误；故选：C．

查看答案和解析>>

科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章达标检测卷 题型：单选题

阅读材料：因为cos 0°＝1，cos 30°＝，cos 45°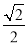＝，cos 60°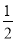＝，cos 90°＝0，所以，当0°＜α＜90°时，cosα随α的增大而减小．解决问题：已知∠A为锐角，且cos A＜，那么∠A的取值范围是(　　)

A. 0°＜∠A＜30° B. 30°＜∠A＜60° C. 60°＜∠A＜90° D. 30°＜∠A＜90°

C 【解析】根据余弦值的阅读材料，可由0＜cosA＜，得cos90°＜cosA＜cos60°，故60°＜∠A＜90°. 故选：C.

查看答案和解析>>

科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章达标检测卷 题型：单选题

在Rt△ABC中，∠C＝90°，AB＝10，AC＝6，则cos A的值是(　　)

A. 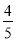B. C. D.

B 【解析】由余弦定义可得cosA＝，因为AB＝10，AC＝6，所以cos A＝. 故选：B.

查看答案和解析>>

科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

如图，在△ABC中，点P、Q分别是BC、AC边上的点，PSAC，PRAB，若AQPQ，PR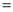PS，则下列结论：①ASAR；②QP∥AR；③△BRP ≌△CPS；④S四边形ARPQ=．其中正确的结论有____________（填序号）.

①② 【解析】连接AP. ∵PR=PS，AP=AP，PR⊥AB，PS⊥AC， ∴△APR≌△APS， ∴AS=AR，①正确. ∵PR=PS，PR⊥AB，PS⊥AC， ∴AP是∠BAC的平分线， ∴∠BAP=∠QAP. ∵AQ=PQ， ∴∠QAP=∠QPA， ∴∠BAP=∠QPA， ∴QP∥AR，②正确. 点P是BC的上的点，并...

查看答案和解析>>

科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

如图，直线l外有不重合的两点A、B．在直线l上求一点C，使得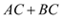的长度最短，作法为：①作点B关于直线l的对称点B＇．②连接AB＇交直线l于点C，则点C即为所求．在解决这个问题时，没有用到的知识点是( )

A. 线段的垂直平分线性质 B. 两点之间线段最短

C. 三角形两边之和大于第三边 D. 角平分线的性质

D 【解析】【解析】 ∵点B和点B′关于直线l对称，且点C在l上， ∴CB=CB′. ∵AB′交l于C，且两条直线相交只有一个交点， ∴CB′+CA=AB′，即CA+CB=AB′. 任取直线l上一点C′，与点C不重合，则C′B′+C′A＞AB′，即AB′是CA+CB的最小值. 本题在解答过程中利用了线段垂直平分线的性质定理：两点之间，线段最短，体现了转化思想...

查看答案和解析>>

科目：初中数学 来源：2017-2018学年七年级数学北师大版上册第1章丰富的图形世界单元测试卷 题型：填空题

从正面、左面、上面看一个几何体得到的形状图完全相同，该几何体可以是________． (写出一个即可)

答案不唯一，如：球、正方体等【解析】【解析】球从正面看是圆形、从左面看是圆形、从上面看圆，符合题意．故答案为：答案不唯一，如：球、正方体等．

查看答案和解析>>

科目：初中数学 来源：江苏省扬州市2018届九年级上学期期末考试数学试卷 题型：解答题

制造弯形管道时，经常要先按中心线计算“展直长度”，再下料.右图是一段弯形管道，其中∠O=∠O＇=90°，中心线的两条弧的半径都是1000mm，这整段变形管道的展直长度约为（π取3.14）（）

A. 6140mm B. 6280mm C. 9280mm D. 457mm

A 【解析】图中管道的展直长度=2×+3000=1000π+3000≈1000×3.14+3000=6140mm．故选A．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学