
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2 | D. | 1 |
分析 先根据已知条件判定△E'A'B∽△ABC,得出∠A'BE'=∠ACB,进而判定AC∥BE',连接BN,则△AMN的面积=△ABN的面积,根据N为AC的中点,故△ABN的面积为△ABC面积的一半,进而得到△AMN的面积为△ABC面积的一半,即矩形ABCD面积的四分之一,据此可得结论.
解答 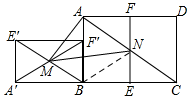 解:由折叠可得,BE=$\frac{1}{2}$BC=AF,而AB:BC=1:$\sqrt{2}$,
解:由折叠可得,BE=$\frac{1}{2}$BC=AF,而AB:BC=1:$\sqrt{2}$,
∴$\frac{AF}{AB}$=$\frac{\frac{1}{2}BC}{AB}$=$\frac{\sqrt{2}}{2}$,
由旋转可得,AF=A'E',AB=A'B,
∴$\frac{A'E'}{A'B}$=$\frac{\sqrt{2}}{2}$,
又∵$\frac{AB}{BC}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{A'E'}{A'B}$=$\frac{AB}{BC}$,
又∵∠E'A'B=∠ABC=90°,
∴△E'A'B∽△ABC,
∴∠A'BE'=∠ACB,
∴AC∥BE',
连接BN,则△AMN的面积=△ABN的面积,
由题可得,N为AC的中点,故△ABN的面积为△ABC面积的一半,
∴△AMN的面积为△ABC面积的一半,即矩形ABCD面积的四分之一,
∴△AMN的面积=$\frac{1}{4}$×8=2,
故选:C.
点评 本题主要考查了折叠的性质以及旋转的性质,相似三角形的判定与性质的综合应用,解决问题的关键是依据相似三角形的对应角相等,得出平行线.解题时注意:平行线之间的距离处处相等.


科目:初中数学 来源: 题型:选择题
| 尺寸/cm | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量(双) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
| A. | 方差 | B. | 众数 | C. | 平均数 | D. | 频数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 最高气温(度) | 22 | 23 | 24 | 25 |
| 天 数 | 1 | 4 | 2 | 3 |
| A. | 23.5,23,23.7 | B. | 23,24,23.5 | C. | 24,23.5,25.5 | D. | 23.5,23,23.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
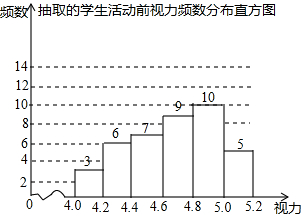 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示 | 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
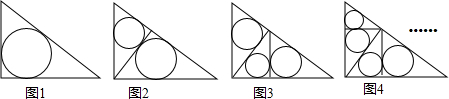
| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
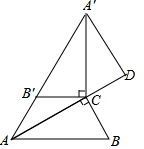 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线C1:y=ax2-4ax-5(a>0).
已知抛物线C1:y=ax2-4ax-5(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
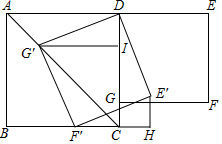 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )| A. | $\sqrt{2}$$+\sqrt{6}$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{3}+\sqrt{2}$ | D. | $\sqrt{3}+\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com